Parte 3: Ángulos y Triángulos
Propuestas didácticas para el estudio de la Geometría en Segundo Ciclo. Material para docentes.
Creado: 28 noviembre, 2022 | Actualizado: 5 de septiembre, 2023
Momentos de esta propuesta:
- 1 Retomar Primer Ciclo.
- 2 Circunferencia y Círculo.
- 3Ángulos y Triángulos.
- 4 Cuadriláteros.
Acerca de la organización del material para alumnas y alumnos
Esta “Parte 3: Ángulos y Triángulos”¹ está organizada en apartados que contienen grupos de problemas sobre diferentes recortes del tema. Los títulos de cada apartado anticipan los contenidos o tipo de trabajo propuesto a las y los estudiantes, por ejemplo, “Problemas para copiar y trasladar medidas” o “Problemas para copiar triángulos”. Estos problemas se proponen para resolver individualmente o, si la o el docente lo considera pertinente, para resolver en parejas. Luego de las resoluciones individuales o en parejas será interesante coordinar momentos de intercambio colectivo en los que sea posible difundir y analizar estrategias, soluciones, errores, conclusiones, etc. En ciertos apartados se ha agregado un subtítulo en letra itálica que informa cuáles son los instrumentos geométricos que será necesario tener disponible para resolver los problemas de ese apartado. Al habilitar o restringir el uso de determinados instrumentos geométricos se busca complejizar o facilitar la resolución de cada problema. Se trata entonces de una de las variables didácticas que las y los docentes podrán considerar para acompañar la diversidad de conocimientos presentes en el aula; incluso, proponiendo el uso de distintos instrumentos a diferentes grupos de estudiantes de manera simultánea. Al mencionar en este subtítulo regla no graduada nos referimos a cualquier objeto que permita trazar líneas rectas sin que sea relevante la graduación en cualquier unidad de medida; en particular puede tratarse de la parte de la regla común que no tiene los números indicadores de centímetros, es decir la parte sin la graduación. Dado que la denominación “regla no graduada” podría ser nueva para las chicas y los chicos, será necesario aclararles qué es y para qué la utilizamos.
Al igual que venimos proponiendo en otros materiales, incluimos instancias de reflexión sobre lo realizado. Estas situaciones plantean un retorno sobre los problemas matemáticos y sobre los diversos procedimientos desplegados para resolverlos, entendiendo que detenerse y volver atrás es fundamental para avanzar, porque los conocimientos movilizados durante la resolución suelen funcionar de manera implícita y podrían permanecer en ese estado de no mediar situaciones que requieran su explicitación. Entre estas instancias de reflexión pueden encontrar las siguientes “Para revisar y resolver” y “Para seguir pensando”. La primera instancia propone la reflexión, el análisis y/o el registro de lo realizado a propósito de un conjunto o subconjunto de problemas de un mismo apartado. Estos nuevos acercamientos a los problemas se proponen en algunos casos de manera individual, en otros en parejas o pequeños grupos, pero también se ofrecen situaciones para resolver entre todas y todos, discutiendo bajo la coordinación de la o el docente y usando el pizarrón o carteles como soportes para el registro. La segunda sección mencionada pretende poner en juego nuevos problemas acerca de lo trabajado y aprendido en el apartado correspondiente; nuevamente se propone trabajar con diferentes organizaciones del grupo en el aula. La diferencia entre estas dos instancias radica en que la primera retoma los problemas para realizar una nueva reflexión, revisión o registro; la segunda, en cambio, ofrece problemas nuevos, diferentes de los anteriores, pero en los que será pertinente poner en juego lo aprendido, lo registrado, lo reflexionado. Presentamos a continuación ejemplos de estas instancias:
Para revisar y resolver (pág. 6)
| ENTRE TODAS Y TODOS. Discutir y registrar una estrategia que permita copiar el triángulo dado sin usar la regla graduada. |
Para seguir pensando (pág. 14)
| -DE A DOS. Con las siguientes medidas de segmentos y sin construir decidan en cada caso si con ellas se puede o no construir un triángulo.
a- 6 cm, 2 cm, 2 cm b- 4 cm, 5 cm, 6 cm c- 4 cm, 6 cm, 10 cm d- 1 cm, 2 cm, 3 cm e- 8 cm, 2 cm, 5 cm -DE A DOS: Propongan medidas de tres lados que estén seguras y seguros que con ellas no se puede construir un triángulo. |
La escritura de conclusiones está planteada en forma colectiva, sin embargo, en otros momentos podría ser propuesta en parejas o pequeños grupos. Las situaciones en que las y los estudiantes le dictan a su docente las conclusiones para que queden en un cartel o en el pizarrón son buenas oportunidades para revisar las ideas iniciales, profundizar el análisis de las argumentaciones, analizar errores. Es importante que esos registros resulten claros para todas y todos, y que puedan reconocer allí aquello que circuló en la clase y que puede ser reutilizado. Esas escrituras podrán ser retomadas y revisadas a medida que se transforman los conocimientos de las y los estudiantes; por lo que será necesario que estén a la vista del grupo, por ejemplo, en carteles en el aula o en carpetas o cuadernos.
Incluimos, asimismo, algunos recuadros con texto y dibujos que podrían actuar de ayuda-memoria, toma de notas u orientaciones para el trabajo, bajo los títulos de “Para recordar” y “Para tener en cuenta al resolver”. Los primeros se proponen con doble intención, por un lado, recordar algunas características o propiedades ya conocidas de las figuras geométricas y, por otro lado, anticipar algo nuevo que será necesario recordar. Para ambos propósitos lo incluido en los recuadros es para “tener a mano” durante la resolución de los nuevos problemas. A continuación, se presenta un ejemplo de estos recuadros:
Para recordar (pág. 14)
| Si un triángulo tiene sus lados iguales a los de otro triángulo, los triángulos son iguales, sin importar la posición en que se encuentren.
Cuando se tiene la medida de tres segmentos no siempre existirá un triángulo que los tenga como lados. Para que exista el triángulo debe cumplirse que la suma de la medida de dos lados debe dar un resultado mayor que la medida del lado que no se sumó. |
Para recordar (pág. 28)
| Los triángulos que tienen un ángulo recto, de 90º, se llaman Triángulos Rectángulos. |
Será importante que esta información esté disponible durante la resolución de nuevos problemas. A su vez, será interesante que las y los estudiantes vayan construyendo desde el primer día del trabajo geométrico una sección dentro de la carpeta que contenga estas ayuda-memoria, esta información valiosa, sistemáticamente ordenada, para acudir a ella cuando sea necesario; al igual que los registros colectivos mencionados en el párrafo anterior.
Los recuadros “Para tener en cuenta al resolver” apuntan a tomar nota de cómo usar ciertos instrumentos geométricos para la construcción o trazado de objetos geométricos, por ejemplo, regla no graduada, escuadra, transportador. También se incluyen en estos recuadros notas para recordar alguna de las propiedades o características trabajadas. A continuación, se presenta un ejemplo de estos recuadros, que se encuentra en la página 18:
| Para tener en cuenta al resolver: Para copiar y medir ángulos de 90 grados se puede usar escuadra. Para ángulos de otras medidas se puede usar el transportador o varillas articuladas. |
La variedad de modalidades de organización también representa un recurso potente para dar lugar a las diversas voces y conocimientos de las chicas y los chicos. En ocasiones, es importante reservar un primer acercamiento individual para que cada estudiante tenga un espacio propio para analizar el problema geométrico propuesto, movilice los conocimientos que considere pertinentes y ensaye un primer camino de resolución. En otras, el trabajo individual se plantea al final de un conjunto de clases con la intención de favorecer una mayor autonomía para usar lo que se aprendió luego de un tiempo de estudio. Asimismo, es importante ofrecer momentos de trabajo con otras y otros dada la potencialidad de las interacciones entre pares para la construcción y el avance de los conocimientos.
Sobre el uso de los instrumentos geométricos
Incluimos en algunos apartados y/o problemas el uso de algunos de los instrumentos geométricos que las niñas y los niños deben utilizar para copiar o construir dibujos que representan objetos geométricos. Es central en el Segundo Ciclo analizar el papel que juega la medición dentro de los problemas geométricos. Medir empíricamente siempre implica la presencia de errores, es decir, las mediciones pueden ser más o menos precisas, pero nunca exactas; por tal razón, cualquier argumento basado en mediciones tendrá un componente de aproximación. En cambio, es necesario pasar progresivamente a argumentos basados en propiedades o características de la figura en cuestión y no del dibujo particular realizado. Por ejemplo, si el problema está centrado en la búsqueda de la amplitud de un ángulo a partir de la medición con el transportador y diferentes niñas y niños dicen “mide 61º”, o “mide 59º”, o “mide 60º”. Será necesario discutir con la clase que todas esas mediciones son aproximadas.
A lo largo del segundo ciclo, el trabajo con compás, transportador, regla graduada, regla no graduada y escuadra se constituye en un valioso recurso para la enseñanza y el estudio de ciertas propiedades de las figuras. Es necesario, por lo tanto, enseñar a utilizarlos sin perder de vista el propósito que tienen. Si bien en los problemas que abordan la construcción de ángulos del material para estudiantes no se presentan situaciones “para enseñar a usar el transportador”, se espera que las maestras y los maestros destinen un tiempo breve para analizar “cómo se usa”, “de qué manera se ubica”, “desde qué parte se empieza a medir”, etc. Sin embargo, se incluye un recuadro explicativo con la intención de ayudar al momento de su presentación en el aula. Como puede verse a continuación:
Usar el transportador (pág. 18)
Para medir o construir ángulos se puede utilizar el transportador. Su escala indica la medida de los ángulos en grados.

En estos casos puede leerse que los ángulos miden 80º.
Sobre el contenido y la organización del documento
La propuesta que presentamos en esta oportunidad aborda la enseñanza de las figuras geométricas. Detallamos a continuación los contenidos incluidos:
- Resolver problemas que demandan comparar y medir ángulos usando escuadra y transportador.
- Construir triángulos a partir de diferentes datos y determinar la cantidad de soluciones posible.
- Explorar la propiedad de la suma de los ángulos interiores de los triángulos.
- Explorar la propiedad de los triángulos acerca de que la suma de dos lados debe ser mayor que el tercer lado.
- Construir y analizar construcciones de triángulos a partir de las medidas de lados y/o ángulos. Analizar la cantidad de soluciones posibles a partir de los datos dados y apelando a las propiedades de la suma de los lados de los triángulos y de la suma de los ángulos interiores de los triángulos. Analizar las clasificaciones de triángulos por lados y por ángulos (sin necesidad de memorizarlas).
En la misma línea que venimos planteando en los materiales producidos por la Dirección Provincial de Educación Primaria entre 2020 y 2022 (entre los que se encuentran las propuestas de intensificación de la enseñanza), los problemas que se incluyen proponen una progresión y secuenciación que apuntan a movilizar ciertos conocimientos con la intención de generar avances en los aprendizajes. Es importante tener en cuenta, entonces, que las y los estudiantes ingresan a estos contenidos a partir de lo que saben acerca de las figuras geométricas y que han construido tanto dentro de la escuela como fuera de ella. Es posible entonces anticipar que los procedimientos iniciales de copiado y construcción de figuras que las niñas y los niños desplieguen tendrán un fuerte anclaje en los conocimientos que han elaborado al resolver otros problemas similares. Cada docente podrá reconocer que para algunas y algunos estudiantes no será necesario detenerse por mucho tiempo en esas propuestas menos complejas dado que las resuelven sin dificultad. Sin embargo, es posible que para otras y otros sea preciso destinar un poco más de tiempo a estudiar aquello con lo que no han tenido oportunidades suficientes de interactuar en años anteriores, para que la producción de nuevos conocimientos les permita ingresar al mundo de los problemas geométricos.
En el material para estudiantes se encuentran los siguientes apartados que dialogan con los contenidos que se enseñan en segundo ciclo y que fueron mencionados anteriormente:
- En los apartados Problemas para copiar y trasladar medidas, Problemas para copiar triángulos, Problemas para construir triángulos, Los triángulos y sus lados se apunta al trabajo relacionado con construir triángulos a partir de diferentes datos y determinar la cantidad de soluciones posible; también explorar la propiedad de los triángulos acerca de que la suma de dos lados debe ser mayor que el tercer lado.
- En los apartados Estudiar los ángulos, Los triángulos y sus ángulos, Los triángulos, sus ángulos y lados el trabajo gira en torno a resolver problemas que demandan comparar y medir ángulos usando escuadra y transportador, así como explorar la propiedad de la suma de los ángulos interiores de los triángulos y analizar las clasificaciones de triángulos por lados y por ángulos (sin necesidad de memorizarlas).
- El último apartado, Nuevos problemas con triángulos, propone integrar el trabajo antes realizado a partir de construir y analizar construcciones de triángulos a partir de las medidas de lados y/o ángulos, así como analizar la cantidad de soluciones posibles a partir de los datos dados y apelando a las propiedades de la suma de los lados de los triángulos y de la suma de los ángulos interiores de los triángulos.
El conjunto de problemas que propone cada apartado contribuye a la construcción y problematización del siguiente. Es así que las situaciones iniciales que se presentan en cada caso, habilitan el uso de los conocimientos que las niñas y los niños puedan tener disponibles a partir de lo movilizado anteriormente.
A continuación, presentaremos algunas orientaciones didácticas para apartados individuales.
Orientaciones didácticas
Si bien las situaciones de los apartados Problemas para copiar y trasladar medidas y Estudiar los ángulos no abordan de manera explícita el trabajo en torno a triángulos, involucran conocimientos que colaboran con el estudio de estas figuras.
Así, en el apartado Problemas para copiar y trasladar medidas (pág. 2) se propone trabajar con la regla no graduada y el compás para poder trasladar medidas o compararlas sin necesidad de obtener un número con la regla graduada. El problema 1 (pág. 2) solicita realizar la copia de segmentos sin definir qué instrumentos usar, por lo que es posible que, en un principio, las y los estudiantes no recurran a los instrumentos mencionados. Teniendo en cuenta esto último, será útil gestionar una puesta en común de las estrategias usadas en la resolución, antes de avanzar con los siguientes problemas del apartado. Así se espera que en la discusión grupal se registre, en carteles para el aula y las carpetas o cuadernos, la utilidad del compás² y de la regla no graduada.
En el problema 2 (pág. 2) y en el problema 3 (pág. 3) se solicita realizar las tareas usando el compás, pues se espera que comiencen a poner en juego lo conversado en torno al problema anterior.
El problema 4 (pág. 3), al igual que el problema 5 (pág. 4) y el problema 6 (pág. 4), no indica qué instrumentos usar, sin embargo, se espera que tengan en cuenta la utilidad del compás para trasladar medidas y de la regla no graduada para asegurar líneas rectas. Este trabajo pretende abonar a ideas que luego serán recuperadas para las construcciones de diversas figuras (triángulos en esta Parte 3 y cuadriláteros en la Parte 4) y para la determinación de la existencia o no de triángulos a partir de segmentos cuya longitud está dada. La regla no graduada, posiblemente un instrumento nuevo para la gran mayoría de las y los estudiantes, se introduce para asegurar líneas rectas, pero inhabilitando la cuantificación de la medición.
Como decíamos al inicio de estas orientaciones, el apartado Estudiar los ángulos (pág. 18) ofrece situaciones por fuera del trabajo con triángulos que permitirán avanzar sobre el conocimiento de los ángulos, para luego utilizarlo en la resolución de situaciones que involucren triángulos. El problema 1 (pág. 18) presenta la oportunidad de emplear escuadras para determinar si los ángulos dibujados son mayores, menores o iguales al ángulo de 90º. En esta instancia alcanza con usar el vértice de la escuadra que se encuentra en el ángulo recto; sin embargo, podría ponerse a discusión que existen distintos tipos de escuadras y que algunas de ellas permiten medir aproximadamente la amplitud de ángulos de 30º y 60º mientras que otras permiten medir ángulos de 45°. Algunas estrategias de resolución que podrían usar las niñas y los niños ante este problema 1 refieren a observar si “sobra parte del ángulo por fuera de la esquina de la escuadra” o si “el ángulo entero queda dentro de la esquina de la escuadra”, esto indicaría que el ángulo es mayor o menor que 90º, respectivamente. Nótese que de esta manera no es necesario recurrir al uso del transportador, sin embargo, algunas chicas y algunos chicos podrían utilizarlo.
Los problemas 2 y 3 (pág. 19) solicitan copiar dibujos. Para realizar la copia del problema 2 las niñas y los niños podrían recurrir a una escuadra, pero si no reconocen su utilidad podrían apelar a cualquier objeto que tenga “esquinas como el cuadriculado de la hoja” (ángulos rectos). Así mismo, podrían reproducir la imagen en hoja cuadriculada aprovechando esas “esquinas”. En este caso es posible que las longitudes de los segmentos no permitan iniciar y terminar en las líneas del cuadriculado por lo que deberán poner en juego otras estrategias. Para el problema 3 la cuestión es más compleja, porque ya no sirve el cuadriculado de la hoja y es poco probable que encuentren a su alrededor objetos con ángulos iguales a los de la poligonal dada. Ante estas dificultades es posible que algunas chicas y algunos chicos pregunten si hay algo con lo que puedan copiar la misma amplitud o apertura; en esos momentos se los podrá remitir al recuadro inicial de este apartado y proponer que busquen un modo en el que el transportador las y los ayude a realizar la copia.
En el recuadro Para revisar y resolver (pág. 19-20) se propone superponer copia y original para cada uno de estos dos problemas y así validar si las copias son o no correctas. Ante aquellas situaciones en las que las copias no sean correctas es posible que algunas chicas y algunos chicos, trabajando individualmente, no puedan definir en qué fallaron, por lo que las puestas en común de la superposición de originales y copias, en pequeños grupos o en parejas, podrá ayudar a analizar y obtener conclusiones. Luego, se les propondrá realizar las copias nuevamente.
En los siguientes tres problemas se propone un trabajo exploratorio respecto de la medida de los ángulos, sin esperar que las niñas y los niños utilicen el transportador como primera estrategia para la resolución. Particularmente, el problema 4 (pág. 20) pide determinar cuál ángulo tiene mayor amplitud. Es posible que algunas chicas y algunos chicos, en lugar de comparar la amplitud, comparen el largo de los “lados” o “segmentos”; si esto sucede será necesaria la aclaración de la o el docente acerca de que no son “lados” ni “segmentos”, pues las “puntas de flecha” indican que las líneas se extienden y no tienen una longitud definida (es decir, son semirrectas). Una estrategia para definir cuál es el ángulo de mayor amplitud podría basarse en recortar o copiar las mismas imágenes, superponerlas haciendo coincidir una de las semirrectas de cada ángulo y observar la semirrecta de cuál de los ángulos queda por dentro del espacio que delimita el otro ángulo. A partir de allí definir que el ángulo que queda por dentro es el de menor amplitud.
4. Decidí cuál de los dos ángulos dibujados es mayor.
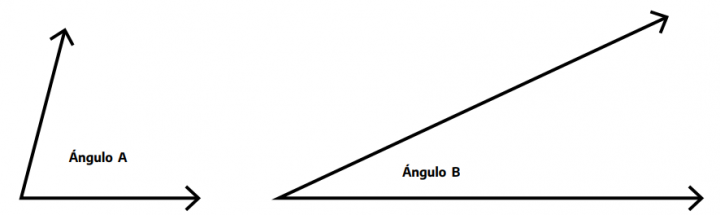
Podrá servir de verificación el uso del transportador o de varillas articuladas.
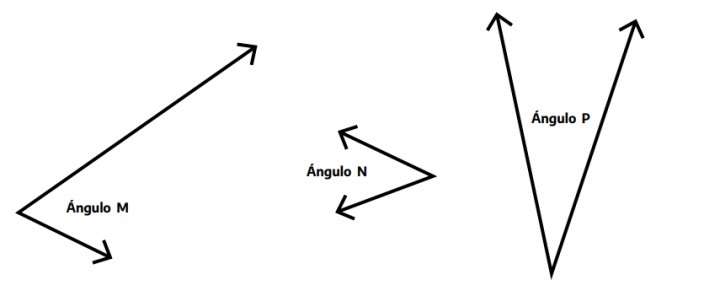
Los problemas 5 y 6 (pág. 20-21) presentan una nueva oportunidad para poner en juego que la amplitud de los ángulos es independiente del largo de los segmentos que se dibujan para representarlos. Así, en el problema 6 el ángulo N tiene mayor amplitud que el P, sin embargo, hemos dibujado segmentos más cortos para representar las semirrectas que lo conforman. Por lo mismo, hemos escogido dibujar segmentos de diferente longitud para representar las semirrectas del ángulo M. Será necesario conversar con las niñas y los niños acerca de esto y, si ellas y ellos lo requieren, pueden prolongarse los segmentos dibujados de manera que todos midan lo mismo; aunque no sea un requisito para determinar el orden según su amplitud.
6.Ordenar los siguientes ángulos de menor a mayor.
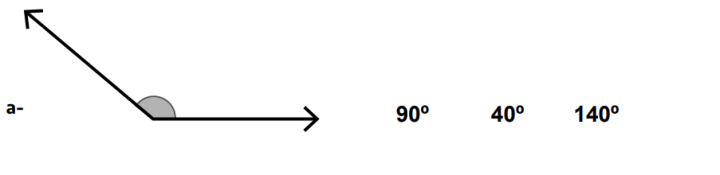
Si bien en el problema 7 (pág. 21) no se pide que expliquen sus decisiones, se espera que las niñas y los niños den argumentos luego de elegir la medida para cada inciso. Por ejemplo, para el inciso a- podrían decir “tiene que ser más grande que 90º porque es más amplio/grande que la escuadra, entonces es de 140º”. Con esto puede verse que no es necesaria la validación con el transportador, aunque las maestras y los maestros podrían incluirlo como parte de la discusión colectiva del trabajo.
7. a- ¿Cuál creés que podría ser la medida de cada uno de los siguientes ángulos? Primero marcá la opción que elegiste y luego comprobá la amplitud del ángulo con el transportador.
Los problemas 8 y 9 (pág. 22) tienen la intención de poner en práctica el uso del transportador, construyendo los ángulos pedidos.
Con los párrafos precedentes estuvimos ofreciendo orientaciones didácticas referidas a los dos apartados que tratan conocimientos que se requieren para el trabajo con triángulos, aunque no se propongan situaciones que los involucren. A partir del próximo párrafo ingresamos al análisis de los apartados que explícitamente consideran el estudio de los triángulos y sus propiedades.
Con el apartado Problemas para copiar triángulos (pág. 5) se apunta a un trabajo sobre el copiado utilizando la regla no graduada y el compás. El problema 1 (pág. 5) propone realizar la tarea de un modo exploratorio, aunque será útil tener en cuenta lo resuelto en el apartado anterior pues para trasladar la medida de los lados sin usar la regla graduada servirá usar el compás. Luego de la resolución de este problema se propone el recuadro Para revisar y resolver (pág. 6), en el que se solicita la discusión grupal acerca de las estrategias usadas, de manera que aquellas y aquellos estudiantes que hayan tenido más dificultades en la realización de la copia puedan escuchar y analizar el modo de resolución elegido por sus compañeras y compañeros. Además, podría servir escribir un cartel con algunas conclusiones, que quede en el aula y en las carpetas o cuadernos, para ser consultado frente a los demás problemas en los que es necesario copiar o construir triángulos, no solo de este apartado. Estas ideas podrán ser retomadas al resolver el problema 2 (pág. 7).
Con el apartado Problemas para construir triángulos (pág. 8) se avanza sobre el estudio de las condiciones que deben cumplirse, en relación con las longitudes de los lados, para que un triángulo exista. Es decir, se proponen situaciones en las que debe investigarse la relación entre las longitudes de segmentos para que ellos sean los lados de un triángulo que exista. El conjunto de problemas 1, 2 y 3 (pág. 8-9) prepara el terreno para abordar la resolución de los problemas 4, 5 y 6 (págs. 9-10). Así, el primer grupo de problemas apunta a la construcción de triángulos a partir de trasladar segmentos (como se pide realizar la tarea en la carpeta o cuaderno, no podrán usar los segmentos dados sino una copia de ellos). En los problemas 1 y 2 se espera el uso del compás para realizar la tarea. Ambos problemas admiten más de una construcción posible, en el caso del primero de ellos porque solo se da la medida de un lado, por lo que puede elegirse la medida de los otros dos y de los ángulos entre muchas opciones posibles. En el caso del segundo problema, la multiplicidad de posibilidades radica en el ángulo que escojan entre los segmentos copiados, lo que determinará muchas opciones distintas para la medida del tercer lado. Presentamos dos posibles construcciones a partir de los segmentos dados en el problema 2 y esperamos que durante la discusión colectiva se generen intercambios en torno a las diferentes construcciones que podrían surgir en el aula.
2. Construí, en tu carpeta, un triángulo que tenga un lado del mismo largo que el segmento BF y otro lado del mismo largo que el segmento TP, sin usar la regla graduada.



El conjunto de problemas 4, 5 y 6 solicita nuevamente la construcción de triángulos conociendo uno, dos y tres lados, respectivamente, pero esta vez esa información se ofrece como una medida en centímetros. Además, se agrega la pregunta ¿cuántos distintos pueden construirse?, lo que apunta a reflexionar sobre los largos de los lados que no fueron dados como dato. Si hubo discusiones colectivas respecto de la resolución de los problemas 1, 2 y 3, aquellas conversaciones y conclusiones podrían servir para explicar en estos nuevos problemas la respuesta relacionada con la cantidad de construcciones posibles.
En los problemas 7, 8 y 9 (págs. 10-11-12) se introduce una primera aproximación a la propiedad triangular. Es posible que, en las instancias iniciales, ante la incógnita de si es o no posible cada construcción, las y los estudiantes utilicen argumentos vinculados a las propias posibilidades de construcción y no a la existencia del triángulo correspondiente. Así podrían decir, por ejemplo, “no me sale” o “no puedo construirlo”, y que su imposibilidad se deba a cuestiones ligadas a no saber cómo hacerlo o a no haber sido suficientemente precisa o preciso en las mediciones. Por lo tanto, se espera que a partir del análisis colectivo de lo trabajado las niñas y los niños puedan establecer el carácter necesario de la relación entre los lados y conjeturar “no se puede construir porque no se llegan a tocar los dos lados cortos” o “con dos lados puedo construir muchos triángulos distintos”, entre otras. Una de las ideas que se espera que puedan elaborar es en relación a la igualdad de los triángulos. Es decir, si un triángulo tiene sus lados iguales respectivamente a los lados de otro triángulo, estos son iguales, sin importar que estén ubicados en diferentes posiciones. Otra idea que esperamos que puedan construir las niñas y los niños es que no es suficiente con saber la medida de tres segmentos para que con ellos se pueda construir un triángulo.
La sección siguiente, Para revisar y resolver (pág. 12-13), promueve la escritura entre todas y todos de ideas generales, aplicables a otras situaciones, en especial el último de los ítems incluidos:
| Vuelvan a mirar los problemas 7, 8 y 9. Escriban un texto que les ayude para, en nuevos problemas, saber en qué casos es posible la construcción y en qué casos no lo es. |
Una vez resueltos estos ítems colectivamente, se propone abordar en parejas los problemas de la sección Para seguir pensando (pág. 14), que tienen la intención de poner en práctica en nuevas situaciones aquello que se discutió y concluyó a propósito de los puntos anteriores.
El recuadro Para recordar (pág. 14) se incluye allí para que sea discutido por el grupo clase completo luego de la resolución de los problemas precedentes, incluida la instancia de reflexión Para revisar y resolver y la de reinversión Para seguir pensando. Es importante tomar nota de estos argumentos ya que serán puntos de partida para próximos problemas, aunque en el material no se explicita, se podría confeccionar colectivamente un cartel para el aula y para las carpetas o cuadernos y volver a él cuando sea necesario.
Para recordar (pág. 14)
| Si un triángulo tiene sus lados iguales a los de otro triángulo, los triángulos son iguales, sin importar la posición en que se encuentren.
Cuando se tiene la medida de tres segmentos no siempre existirá un triángulo que los tenga como lados. Para que exista el triángulo debe cumplirse que la suma de la medida de dos lados debe dar un resultado mayor que la medida del lado que no se sumó. |
El apartado Los triángulos y sus lados (pág. 15) avanza hacia la caracterización de triángulos según la medida de sus lados, aportando desde el inicio la clasificación habitual en un recuadro Para recordar (pág. 15). Podría ser útil que este recuadro quede a la vista de todo el curso en las paredes del aula como así también en las carpetas o cuadernos, de manera que pueda ser consultado siempre que se necesite. Se trata de que las y los estudiantes identifiquen en un triángulo isósceles, equilátero o escaleno las características que permiten definirlos. Se formulan problemas de construcción en los que no solo se ofrecen como dato las longitudes de algunos lados, sino que también se informa sobre el tipo de triángulo que se busca construir, como en el caso del problema 1 (pág. 15):
a- Construí un triángulo equilátero cuyos lados midan 4 cm.
b- ¿Hay un solo triángulo posible o más?
Con este problema se pretende poner en discusión no solo que para construir triángulos equiláteros se requiere la medida de un lado, sino que además se espera volver a conversar acerca de la igualdad de triángulos con la medida de los lados prefijada sin importar la posición relativa a la hoja, en particular esta vez para triángulos equiláteros. Si bien se trata de una validación empírica, la o el docente podrá proponer superponer las construcciones de diferentes estudiantes para determinar su igualdad.
Así mismo, en el primer ítem del recuadro Para revisar y resolver (pág. 17) se pone en discusión la inclusión de los triángulos equiláteros dentro de la clasificación de isósceles. Considerando que al inicio de este apartado se ha definido a los triángulos isósceles como aquellos con al menos dos lados de la misma medida, será interesante conversar con las chicas y los chicos acerca de la frase “al menos dos”. Esta no restringe a solamente dos sino que se abre hacia la posibilidad de que los tres lados midan lo mismo. Esta situación de unas figuras incluidas dentro de la clasificación de otras, porque cumplen con las definiciones aportadas, volverá a ser relevante en el estudio de cuadriláteros; por lo que se espera se guarde memoria y registro de lo aquí conversado.
El material para estudiantes continúa con el apartado Estudiar los ángulos, que fue analizado páginas atrás, por lo que avanzaremos al conjunto de problemas que aborda el estudio de ángulos en relación directa con los triángulos. Este apartado, denominado Los triángulos y sus ángulos (pág. 24), permite analizar y profundizar, luego de un trabajo exploratorio, la propiedad relacionada con la suma de los ángulos interiores de todo triángulo. Los problemas 1, 2, 3 y 4 (págs. 24-25-26) están pensados para sostener el trabajo exploratorio, ya que las construcciones involucran la medida de los ángulos interiores y la imposibilidad de unir los segmentos-lados cuando la suma de los ángulos dados sea mayor a 180º. Esto da lugar, en algunos casos, a un análisis de la cantidad de soluciones, un tipo de práctica inherente a la actividad geométrica que se pretende instalar. Por ejemplo, en el problema 1 (pág. 24) se ofrecen ternas de ángulos para la construcción de triángulos. Algunas de estas construcciones no son posibles, cuestión que podrá ser discutida y justificada en un intercambio colectivo. Esta discusión se propone luego de resolver los problemas 2, 3 y 4 y antes de leer y analizar el recuadro Para tener en cuenta al resolver (pág. 26). Es probable que en un principio las justificaciones infantiles se vinculen a su propia experiencia, así podrían decir “no me sale” o “no puedo construirlo”. Esto puede deberse a que no saben cómo seguir luego de trazar dos ángulos o cómo decidir si el tercer ángulo mide o no lo que se ofrece; es decir, cuestiones no vinculadas a la existencia o no de los triángulos. Se espera que a partir del análisis colectivo de lo trabajado, las niñas y los niños puedan establecer el carácter necesario de la relación entre los ángulos y conjeturar “no se puede construir porque no se llegan a tocar los dos lados” o “si dibujo dos ángulos, el tercero no se forma”, entre otras.
1. A veces es posible construir triángulos dados los ángulos y a veces no lo es. Usando el transportador construyan, si es posible en cada caso, un triángulo con las medidas de ángulos que se proponen.
a- 30°, 50°, 100°
b- 40°, 40°, 40°
c- 90°, 50°, 70°
d- 60°, 60°, 60°
En el problema 2 (pág. 25) se pide solo una explicación, sin embargo, es posible que algunas chicas y algunos chicos intenten la construcción a pesar que se anticipa que no es posible. Será necesario reflexionar en torno a dichos intentos. En el problema 3 (pág. 26) no se anticipa la imposibilidad, pero se pregunta por la medida del tercer ángulo. Posiblemente las y los estudiantes primero procuren la construcción y luego intenten medir el ángulo que no fue dado. Así, algunas y algunos estudiantes dirán que pudieron realizar la construcción y que el ángulo solicitado podría medir muy pocos grados. Nuevamente, será necesario propiciar reflexiones en torno a esos intentos y arribar, por ejemplo, a conclusiones como la siguiente: “si en los dos vértices del lado que dan trazo ángulos de 90º, no podré determinar el tercer ángulo, porque nunca se tocarán los últimos dos lados que dibujé por más que los prolongue”. Es necesario resaltar que las construcciones con instrumentos de medida podrían arrojar como conclusión que puede trazarse un triángulo que en realidad no existe, porque las mediciones son siempre imprecisas. Por este motivo se promueven validaciones racionales, sabiendo que irán aproximándose a ellas progresivamente.
Notarán que luego del problema 4 se incluyó una ayuda para el análisis que sigue, el recuadro Para tener en cuenta al resolver (pág. 26). La decisión de incluir allí esa “interrupción”, por decirlo de un modo coloquial, se basa en la necesidad de sistematizar la propiedad que fue objeto de estudio en los problemas precedentes y, a la vez, ofrecer un apoyo teórico para las reflexiones que se proponen en la sección Para seguir pensando (pág. 27). Se espera que las y los estudiantes puedan comprender esta relación, no sólo para conocerla, sino también como un modo de trabajo argumentativo sobre las propiedades de las figuras geométricas en general, de los triángulos en particular. Será importante retener y tener disponible este registro.
Los problemas 5 y 6 (pág. 28) funcionan como situaciones de reinversión de lo trabajado, para las cuales servirá usar las conclusiones a las que se arribó. Se incluye una sistematización breve acerca de las ideas que se estuvieron estudiando a partir de los apartados anteriores.
El conjunto de problemas del apartado Los triángulos, sus ángulos y lados (pág. 30) resultan de mayor complejidad dado que se busca poner en juego lo estudiado sobre triángulos tanto en relación a sus lados como a sus ángulos; asimismo deberán considerar propiedades o definiciones para obtener resultados sin tener que realizar construcciones, en algunos problemas. Por ejemplo, en el problema 1a (pág. 30) deberán apelar a la propiedad ya presentada y estudiada de la suma de ángulos interiores para determinar la medida del ángulo que no se conoce en cada figura. Si bien se espera que no sea necesario medir con transportador para decidirlo, es probable que algunas chicas y algunos chicos recurran a ello para verificar su anticipación. Podría ser relevante que esto se converse con el grupo y que se pueda concluir que si se cumple la propiedad a partir de los cálculos resueltos (por ejemplo, restar cada ángulo dado a 180º), entonces no es necesario verificar con el instrumento, alcanza con los argumentos apoyados en la propiedad.
Así mismo, se ha incorporado el ítem b y el ítem c de este mismo problema 1 para iniciar un camino exploratorio -que sigue con el siguiente recuadro Para seguir pensando (pág. 31-32)- a través del cual esperamos puedan reconocer que la clasificación isósceles se define por la medida de los lados, pero también implica que habrá ángulos con medidas iguales. A partir de allí podría proponerse analizar qué sucede con los ángulos en los triángulos escalenos y finalmente en los equiláteros. Algunas de las conclusiones a las que podrían arribar, en palabras de las niñas y los niños, son: “si tiene dos lados iguales, también tiene dos ángulos iguales, y es isósceles”, “si tiene todos los ángulos distintos, tiene todos los lados distintos, y es escaleno”. Esto último podría engrosar las afirmaciones teóricas expresadas en el ayuda-memoria de la página 29, así como los carteles del aula y de las carpetas o cuadernos, agregando a cada clasificación una expresión como “también se cumple que al menos dos ángulos son iguales” -para el caso de los isósceles-, “también se cumple que los tres ángulos son distintos” -para el caso de los escalenos- y “también se cumple que los tres ángulos son iguales” -para el caso de los equiláteros-.
Con el problema 2 (pág. 32) se intenta poner en relación la condición que deben cumplir los lados del triángulo para que sea isósceles con la propiedad triangular. Al ofrecer las medidas de dos lados es posible anticipar que el tercero podría medir lo mismo que uno u otro de ellos. Luego será necesario analizar si en ambos casos se cumple que la suma de la medida de dos lados dé por resultado un número mayor que la medida del lado no sumado. En este caso se cumple para las dos posibilidades, pues la terna de medidas de lados podría ser 6 - 4 - 4 o 6 - 6 - 4, cumpliéndose las dos veces la propiedad mencionada. Este problema puede resolverse mediante las anticipaciones expresadas, y no será tarea simple realizarlas; podría ser de utilidad conversar entre todas y todos luego de tomarse un tiempo de resolución individual, aun cuando haya muchas y muchos estudiantes que no terminen de resolver. En la puesta en común, la o el docente podría iniciar el debate sobre qué debe cumplir el triángulo para asegurar que es isósceles. Recién después de haber conversado y concluido que debe darse que haya dos lados que tengan la misma medida, podría guiar la discusión hacia la necesidad de verificar si existen triángulos con esas dos ternas de medidas de lados. Esto incluso podría ser parte de un cartel para el aula y para los cuadernos o carpetas, en el que se deje asentada la importancia de analizar si se cumple la propiedad mencionada.
Los problemas 3 y 4 (pág. 33) demandan la consideración de construir ángulos mayores o iguales que 90º, respectivamente, siendo que el triángulo que lo contenga será isósceles. La discusión grupal luego de la resolución individual podría girar en torno a la cantidad de triángulos diferentes que existen con esas características, debiendo llegar a concluir que en el caso del ángulo obtuso, como no se informa una medida particular, puede haber muchas amplitudes que cumplan. En cambio, en el caso del ángulo recto, como se define la medida exacta (90º), entonces queda determinado un solo triángulo. No esperamos que se tomen notas referidas a los criterios de congruencia (habitualmente mencionados como LAL y ALA), pero sí que puedan guardar en memoria y en registros que al no tener definida la medida del ángulo obtuso, pudieron elegirse muchos valores diferentes y eso arroja la conclusión de que hay infinitos triángulos posibles; y que al tener determinada la medida del ángulo recto y de los lados que lo forman, no se puede modificar la medida del tercer lado ni la de los otros dos ángulos (aun cuando no sea posible, por ahora, averiguar estas últimas medidas mencionadas).
Los problemas 5, 6 y 7 (págs. 33-34) solicitan construcciones. Si bien no se requieren anticipaciones, ni el análisis de la cantidad de soluciones viables, esto podría ser motivo de algunas conversaciones grupales luego de haber realizado las tareas mencionadas. Es posible que, ante el problema 8, algunas chicas y algunos chicos digan que no es posible construir otro triángulo distinto, como se pide en el ítem b-. En ese caso se podrá evocar el trabajo realizado en problemas anteriores, como el 2 de este mismo apartado. Allí se llegó a concluir que es necesario analizar qué significa isósceles y tener en cuenta una propiedad que asegura la existencia de un triángulo (en aquella oportunidad, referida a la medida de los lados; esta vez, referida a la medida de los ángulos). Así, se les podría pedir que anticipen la medida de los ángulos que no se mencionan, y al ver que hay dos opciones que cumplen que la suma de los tres da 180º (70º - 70º - 40º y 70º - 55º - 55º), se podrán construir dos triángulos distintos.
El último apartado que presentamos, Nuevos problemas con triángulos (pág. 35), contiene una serie de situaciones que pretenden integrar todo lo trabajado en esta Parte 3. Para resolver los problemas que se incluyen será importante tener disponibles los carteles, las conclusiones y las estrategias ya estudiadas y registradas. Es así que encontrarán problemas parecidos a otros resueltos con anterioridad, pero en los que ahora se pide anticipar para responder sin construir; sistematizar algunas ideas; alcanzar generalizaciones. Nuevamente se ofrecen las secciones Para revisar y resolver (pág. 38) y Para seguir pensando (pág. 39); ambas podrían servir como puntapié para la construcción de nuevos carteles, luego de las discusiones grupales, que se utilizarían como ayuda-memoria cuando continúen el trabajo geométrico de la Parte 4 para Segundo Ciclo.
En este documento hemos intentado acompañar el análisis de los problemas del material para estudiantes. Esperamos que su lectura constituya un aporte para la planificación y la gestión de las clases.
¹ Para conocer más sobre el enfoque didáctico que sostiene esta propuesta remitirse a la Parte 1 de esta misma colección: “Retomar Primer Ciclo. Propuestas didácticas para el estudio de la Geometría en Segundo Ciclo. Material para docentes”.
² Tal vez sea necesario para algunas chicas y algunos chicos conversar acerca de cómo se usa el compás; para tal cometido podría ser útil resolver los problemas que ofrecemos bajo el nombre Parte 2: Circunferencia y Círculo, si es que no lo han resuelto ya.
Imagen de portada: Freepik