El trabajo geométrico en Primer Ciclo de la escuela primaria involucra el estudio de las características de las figuras y los cuerpos geométricos. El inicio de la enseñanza por uno u otro de esos objetos ha sido motivo de múltiples y variadas discusiones, sin embargo, no existen en la actualidad razones suficientes que permitan afirmar la conveniencia de ingresar primero por alguno de ellos. Independientemente del orden en que se decida acceder a estos contenidos, resulta indispensable que se destine un tiempo para establecer relaciones entre ambos. Las propuestas que se incluyen en este documento abordan de manera exploratoria el estudio de las características de las figuras geométricas.

Acerca de la enseñanza de la geometría en Primer Ciclo

Durante el Primer Ciclo de la escuela primaria se busca retomar, sistematizar y ampliar los conocimientos que las chicas y los chicos han podido construir sobre las figuras geométricas en su paso por el Nivel Inicial. Este estudio, mayormente exploratorio, involucra algunas características de las figuras geométricas como, por ejemplo, la cantidad de lados y vértices, igualdad o no de los lados, lados rectos y curvos, etc. Luego de esa primera aproximación, se introduce el estudio de cuadrados, rectángulos y triángulos a partir de diversos problemas que promueven el reconocimiento y la explicitación de sus características (tarea que excede y prescinde del dominio de sus nombres). 

Los dibujos¹ se constituyen en un buen punto de partida para iniciar el estudio de las figuras geométricas. Las primeras interacciones con estas representaciones tendrán una impronta exploratoria y perceptiva, sin perder de vista que será preciso abandonarla progresivamente de modo de introducirlos, en Segundo Ciclo, en un trabajo argumentativo, anticipatorio y deductivo que se apoye en las propiedades de las figuras y sin necesidad de comprobación empírica.

Es así que los dibujos ocupan un rol central en las propuestas que aquí se incluyen, entablando un diálogo de ida y vuelta entre esos dibujos y sus descripciones. Este trabajo es necesario dado que no siempre es posible “ver” en el dibujo las características que distinguen a la figura geométrica representada; para poder “verlas” se vuelve necesario participar de instancias de análisis y reflexión. Lo que “se ve” depende de los conocimientos que la persona que “mira” tiene disponibles, es por ello que a medida que esos conocimientos se van transformando, “se verán” características y propiedades diferentes. Una reflexión sostenida permitirá que las y los estudiantes se alejen progresivamente de lo perceptivo para avanzar en el reconocimiento de algunas características que definen a las figuras geométricas que están estudiando. 

Un aspecto importante a tener en cuenta desde la enseñanza es que los dibujos que se incluyan en las diversas situaciones sean variados en sus formas, dimensiones y posiciones respecto de los contornos de la hoja, los carteles o el pizarrón. De este modo, podrían reducirse o evitarse las dificultades que encuentran algunas y algunos estudiantes para reconocer un triángulo porque “está al revés” o las confusiones entre cuadrados y rombos cuando cambian sus posiciones habituales.

Para finalizar estas primeras líneas nos interesa detenernos en un último aspecto que será profundizado a lo largo del documento: la validación de las producciones. Si bien las y los estudiantes de Primer Ciclo no están aún en condiciones de validar racionalmente por medio de argumentos y demostraciones formales, es importante que puedan aprender a validar "por sus propios medios" si sus producciones son o no correctas. Como ya fue mencionado, será importante avanzar progresivamente en la construcción de validaciones racionales, sin embargo, en Primer Ciclo es necesario asumir la posibilidad de hacerlo a través de validaciones empíricas, es decir, pruebas materiales, perceptivas y basadas en la medida, por ejemplo, a partir de la superposición del modelo original y su copia en problemas que involucran copiar o comparar figuras. 

En consonancia con los materiales que se han producido desde la DEP en estos años (2020-2022), las diferentes actividades que encontrarán en estas páginas pretenden ofrecer numerosas oportunidades de aproximarse a un mismo contenido; detenerse por un tiempo a resolver problemas; explorar y comparar diversas resoluciones; analizar errores y explicaciones; revisar producciones propias y ajenas para mejorarlas; proponer argumentos y discutirlos para ampliarlos, transformarlos o ajustarlos; registrar conclusiones; tomar conciencia de lo que se va aprendiendo y de cómo se va usando lo anterior para lo nuevo. En otras palabras, se trata de estudiar matemática en el aula.

Acerca de la organización del material para estudiantes

El material contiene un conjunto de problemas que permiten aproximarse a cierta porción del conocimiento geométrico, en este caso, el estudio de las figuras geométricas. Estos problemas se proponen para resolver individualmente o bien, si la o el docente lo considera pertinente, para resolver en parejas o en grupos. Será interesante gestionar momentos de intercambio colectivo en los que sea posible difundir y analizar estrategias, soluciones, errores, conclusiones, conjeturas, etc.

Al igual que venimos proponiendo en otros materiales, incluimos numerosas instancias de reflexión sobre lo realizado. Estas situaciones plantean un retorno sobre los problemas matemáticos y sobre los diversos procedimientos desplegados para resolverlos, entendiendo que detenerse y volver atrás es fundamental para avanzar, porque los conocimientos movilizados durante la resolución suelen funcionar de manera implícita y podrían permanecer en ese estado de no mediar situaciones que requieran su explicitación. Entre estas instancias de reflexión pueden encontrar las siguientes: “Para revisar y resolver” y “Para seguir reflexionando y aprendiendo”. La primera propone la reflexión, el análisis y/o el registro de lo realizado a propósito de un conjunto o subconjunto de problemas de un mismo apartado. Los problemas de la segunda sección pretenden que las y los estudiantes pongan en juego lo trabajado al resolver nuevos problemas. La diferencia entre estas dos instancias radica en que la primera vuelve sobre los problemas para realizar una nueva reflexión, revisión o registro. En cambio, la segunda ofrece problemas más complejos en los que es necesario reinvertir lo aprendido. Presentamos a continuación algunos ejemplos de ambas propuestas:

Para revisar y resolver (pág. 7)

Para seguir reflexionando y aprendiendo (pág. 12)

La escritura de conclusiones podrá plantearse en forma colectiva, en parejas o pequeños grupos. Las situaciones en las que las y los estudiantes le dictan a la o el docente las conclusiones para ser escritas en el pizarrón o en carteles, son buenas oportunidades para revisar las ideas iniciales que las chicas y los chicos van elaborando o para analizar errores. Es importante que esos registros resulten claros para todas y todos y que puedan reconocer allí aquello que circuló en la clase y que pueda ser reutilizado. Esas escrituras podrán ser retomadas y revisadas a medida que se transforman los conocimientos de las y los estudiantes; por lo que será necesario que estén a la vista de todas y todos.

Incluimos, asimismo, un recuadro bajo el título “Para recordar y tener en cuenta” que podría actuar de ayuda-memoria, toma de notas u orientaciones para el trabajo. En estas instancias se busca presentar tanto elementos o características de las figuras geométricas como instrumentos que posibilitan algunas construcciones. Presentamos a continuación un ejemplo:

Para recordar y tener en cuenta (pág. 3)

La variedad de modalidades de organización también representa un recurso potente para dar lugar a las diversas voces y conocimientos de las y los estudiantes. En ocasiones, es importante reservar un primer acercamiento individual o en parejas para que cada estudiante tenga un espacio propio para analizar el problema geométrico propuesto, movilice los conocimientos que considere pertinentes y ensaye un primer camino de resolución. En otras, el trabajo individual se plantea al final de un conjunto de clases con la intención de favorecer una mayor autonomía para usar lo que se aprendió luego de un tiempo de estudio. Asimismo, es importante ofrecer momentos de trabajo con otras y otros dada la potencialidad de las interacciones entre pares para la construcción y el avance de los conocimientos.

Detallamos a continuación los contenidos incluidos y los apartados en que se organizan los problemas. 

Contenidos geométricos:

• Explorar, reconocer y usar características de figuras para distinguir unas de otras.
• Copiar y construir figuras que contengan cuadrados, rectángulos y triángulos como medio para analizar algunas de sus características.
• Explorar relaciones entre cuadrados, rectángulos y triángulos.

Apartados en que se organiza el documento:

• Problemas para explorar e identificar figuras
• Problemas para copiar y comparar figuras
• Problemas para ampliar y reducir figuras
• Problemas para describir figuras
• Instrucciones para construir figuras
• Figuras usando otras figuras
• Otros problemas para copiar figuras

En la misma línea que venimos planteando en los materiales producidos por la DEP en estos años, los problemas que se proponen apuntan a movilizar ciertos conocimientos que se irán modificando en virtud de su progresión y secuenciación. Para provocar estos avances se hace uso de distintas variables didácticas, entendidas como los cambios que se realizan con la intención de modificar los niveles de complejidad. Por ejemplo, habilitar o restringir el uso de determinados instrumentos geométricos; proponer el uso de hoja cuadriculada o lisa; variar el tamaño del cuadriculado; modificar la colección de figuras con las que se trabaja o los datos que se ofrecen; entre otras.

Atendiendo a que este documento presenta una propuesta ciclada para estos contenidos, será necesario propiciar un trabajo institucional para definir las situaciones  que serán abordadas en cada año del Primer Ciclo y qué variables didácticas entrarán en juego de modo que esa articulación permita, como planteamos anteriormente, un trabajo sostenido y en progresión.

Es importante mencionar, a su vez, que encontramos en esta organización ciclada un recurso potente para considerar la diversidad del aula desde la planificación de la enseñanza. El hecho de que se incluyan en un mismo documento problemas que abordan el mismo contenido pero con distintos niveles de complejidad pone a la o el docente en mejores condiciones de planificar sus clases sin perder de vista los diversos conocimientos que sus estudiantes tienen disponibles. Por ejemplo, tanto en aulas de sección única como en aulas plurigrado, podrían presentarse en simultáneo problemas de copiado en hoja cuadriculada a las y los estudiantes que se enfrentan por primera vez a este tipo de situaciones y problemas de copiado en hoja lisa, cuya complejidad es mayor, a quienes ya han tenido otros acercamientos a este tipo de tareas.

Tal como se propone en el material elaborado para Segundo Ciclo, se podrán utilizar algunas de las actividades que aquí se presentan para retomar el trabajo realizado en Primer Ciclo. Por ello, es recomendable que al finalizar 3er año las y los estudiantes guarden sus carpetas o cuadernos y que la escuela conserve los carteles del aula con sus reflexiones y conclusiones para usarlas de apoyo y recordatorio en años siguientes. 

A continuación presentaremos algunas consideraciones para cada apartado.

Orientaciones didácticas para cada apartado

• Problemas para explorar e identificar figuras

Se propone iniciar el recorrido con Problemas para explorar e identificar figuras (págs. 2-7). Este apartado incluye un conjunto de situaciones problemáticas que promueve la exploración de diversas figuras a partir de la elaboración e interpretación de preguntas o pistas para descubrir cuál ha sido la elegida en el contexto de un juego de adivinación. A partir de las sucesivas interacciones que se producen con las figuras, las preguntas y las respuestas, se espera que las y los estudiantes, avancen en la identificación de algunas de sus características, establezcan relaciones entre figuras e incorporen progresivamente vocabulario específico. El juego de adivinación se presenta a propósito de dos colecciones de figuras, la primera bajo el título “Adivinar figuras” (págs. 2-4) y la segunda, en “Más figuras para adivinar” (págs. 5-7).       

“Adivinar figuras” (págs. 2-4)        

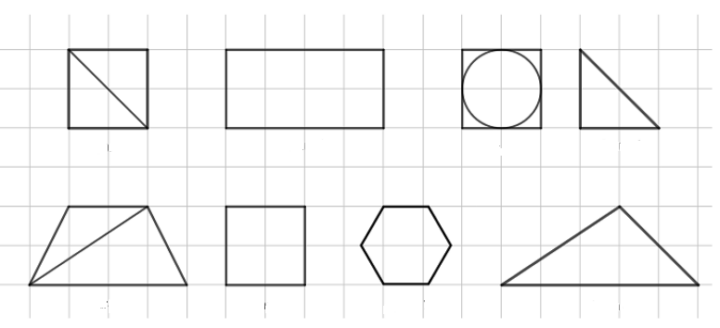
“Más figuras para adivinar” (págs. 5-7)

Las colecciones de figuras seleccionadas resultan una decisión importante en este tipo de actividades y responden al propósito de enseñanza de la o el docente. En este caso, la primera colección promueve gracias a su variedad, que las y los estudiantes se apoyen en la cantidad de lados y vértices, si los lados son o no rectos, etc.; mientras que la segunda tiene la intención de introducir nuevos elementos: diagonales y “figuras dentro de otras”. Se trata de un juego que podrá volver a plantearse con nuevas colecciones de figuras². La conformación de la colección, en tanto puede modificar la complejidad de la tarea y promover la producción de nuevos conocimientos, constituye una variable didáctica.

Otra diferencia que presentan ambas colecciones es el tipo de papel sobre el que están dibujadas: la primera tiene fondo liso y la segunda, cuadriculado. Para algunas o algunos estudiantes el cuadriculado podrá resultar un punto de apoyo, por ejemplo, para determinar la igualdad entre lados.

Es importante agregar que esta situación dejará de ser un verdadero problema si las figuras pueden identificarse por su color, por números o por el material sobre el que fueron construidas (por ejemplo, “¿es la número 2?”, “¿es la roja?”, “¿es la de cartulina?”). Será necesario entonces no añadir a las colecciones presentadas señales que desvíen la atención de las características de las figuras en la que buscamos centrar el debate.

También es importante mencionar que al comenzar el juego es probable que las y los estudiantes asocien las formas de las figuras o sus elementos con objetos de la vida cotidiana (“la que parece una casita”, “la pelota”, “la porción de pizza”, etc.). Estas primeras maneras de nombrar irán dejando paso progresivamente a nuevas descripciones que se apoyan en las características de las figuras.

A grandes rasgos, las propuestas que se presentan en torno a ambas colecciones son semejantes: iniciar jugando, reflexionar sobre las preguntas y las respuestas formuladas en diferentes rondas y resolver una serie de problemas que simulan partidas de juego. La intención sigue siendo la misma: explorar, identificar y explicitar las características de las figuras involucradas. Este recorrido común habilita el planteo simultáneo de diferentes colecciones de figuras en función de la diversidad de conocimientos presente en el aula, sea de sección única o bien plurigrado.

En la sección “Para revisar y resolver” (pág. 3) se propone el intercambio de preguntas formuladas durante el juego con la intención de que las y los estudiantes profundicen el análisis y la caracterización de las figuras. La o el docente podrá registrar las preguntas en un cartel y colaborar en la evocación de las expresiones que circularon a lo largo del juego y que no hayan sido recuperadas por las chicas y los chicos. Esta instancia es también una buena oportunidad para difundir el uso de cierto vocabulario específico utilizado por algunas o algunos estudiantes y que se plasma en los recuadros con información “Para recordar y tener en cuenta”, por ejemplo, vértices, lados rectos y curvos (pág. 3) o diagonales (pág. 6).

Algunos problemas promueven el análisis de pistas para identificar figuras, por ejemplo, el ítem c- del problema 2 (pág. 6).

Será interesante generar un espacio de debate para que las y los estudiantes distingan cuáles informaciones son necesarias y cuáles redundantes o innecesarias, por ejemplo, se espera que identifiquen que si se ofrece la pista “tiene 4 lados” no es preciso aclarar que “tiene 4 vértices”.

Los problemas que se proponen en el apartado “Para revisar y resolver” (pág. 7) buscan que las niñas y los niños, en forma colectiva o en parejas, retomen  los problemas trabajados y reinviertan lo conversado luego de las resoluciones. Esta vez la complejidad está dada por la escritura. Serán ellas y ellos quienes deban escribir preguntas que permitan identificar una sola figura de la colección y, además, agregar un nuevo interrogante que atienda las relaciones establecidas.

• Problemas para copiar y comparar figuras

Este apartado abarca propuestas que involucran la copia de figuras en hoja cuadriculada y la identificación de similitudes y diferencias entre figuras organizadas bajo dos títulos: Problemas para copiar y comparar figuras y Más problemas para copiar figuras. Es importante aclarar que al finalizar el documento para las y los estudiantes se incluye un nuevo apartado que retoma y profundiza este tipo de trabajo al incorporar la copia en hoja lisa: Otros problemas para copiar figuras.

Si se tratara de las primeras interacciones de las niñas y los niños con problemas de copiado de figuras, probablemente las reproducciones no coincidan con las originales en el primer intento. Es por ello que la tarea no se agota en la realización de la primera copia, sino que se propone un trabajo de comparación y revisión de los desajustes como medio para adentrarse en la identificación de las características que es preciso considerar para obtener una figura igual a la dada y analizar las maneras posibles de llevar a cabo esa tarea. Asumir las copias como producciones que pueden revisarse para ir aproximándose sucesivamente a versiones más ajustadas reduce el temor a equivocarse al iniciar la tarea e invita a explorar, analizar e intentarlo nuevamente todas las veces que sea necesario.³ En este sentido, será interesante generar espacios de debate colectivo para dar lugar al análisis de errores y la explicitación de ideas que podrán servir de punto de apoyo al producir una nueva versión de la misma copia o al resolver nuevos problemas. Es importante aclarar que dichas revisiones no pretenden la precisión de las copias en sí mismas, sino que apuntan a ofrecer nuevas oportunidades para analizar las características de las figuras que es necesario considerar para construirlas. Si, en cambio, las y los estudiantes hubieran realizado problemas semejantes a estos en años anteriores, esta colección podrá tomarse como una oportunidad para retomar ese trabajo y avanzar luego, por ejemplo, con el copiado de figuras en hoja lisa. La variación del tipo de hoja no es ingenua, se trata de una variable didáctica que busca generar nuevos desafíos. Volveremos sobre este asunto en el apartado Otros problemas para copiar figuras.

Se espera que el cuadriculado de la hoja se constituya progresivamente en punto de apoyo para realizar las copias: contar cuadraditos para que los lados tengan la misma longitud, dibujar los lados siguiendo las líneas del cuadriculado para que “salgan derechitos”, aprovechar los cruces del cuadriculado para ubicar los vértices y asegurar que “las esquinas queden derechitas”. Estos resguardos dirigidos a lograr una copia del original van focalizando la atención en algunas de las características de las figuras que se espera que comiencen a identificar. La regla podrá constituirse en un buen recurso para trazar líneas rectas.

Los problemas 1, 2 y 3 (pág. 8) apuntan a que las y los estudiantes consideren las características de las figuras para obtener cada copia. Algunas y algunos las tendrán en cuenta al realizar el dibujo; en cambio, otras y otros comenzarán a identificarlas al confrontar copia y original, sobre todo cuando no coinciden (se podría proponer que copien la figura en otra hoja cuadriculada para poder validar la producción superponiéndola a contraluz). Será interesante que la o el docente genere un espacio para analizar de manera colectiva esas discrepancias (“¿por qué no quedaron iguales?”, “está parecida pero más corta”, “quedó medio torcida”, etc.). Dado que el copiado de figuras no exige la verbalización de características de las figuras ni el uso de vocabulario específico, estos dos aspectos podrán ser promovidos a través de instancias colectivas que involucren su explicitación.

En el problema 3 es posible que las niñas y los niños que intenten iniciar la copia trazando la hipotenusa, encuentren dificultades ya que el segmento no coincide con las líneas del cuadriculado ni sigue la diagonal de los cuadraditos. Podrán discutir entre todas y todos acerca de la conveniencia de comenzar trazando los lados que se apoyan sobre las líneas del cuadriculado y unir luego ambos extremos para obtener el tercer lado.

En la sección “Para revisar y resolver” (pág. 9) se propone el intercambio de producciones en parejas para promover la explicitación de los criterios considerados al comparar las figuras originales y las copias de los primeros problemas. Esta tarea se retoma en el problema 4 (pág. 9) al identificar las diferencias entre el rectángulo original y su copia (por ejemplo, “el dibujo original tiene lados más largos que la copia”, “los lados cortos son iguales pero los lados largos no”, “el lado largo es de 8 cuadraditos y en la copia tiene 7”, etc.). Algo similar sucede en el problema 5 (pág. 10), esta vez a propósito de un cuadrado. Se retoma la discusión sobre la medida de los lados, que no coinciden en la copia de Nahuel, y se agrega la necesidad de considerar que las esquinas “queden derechas”, condición que no se cumple en la copia de Ailén.

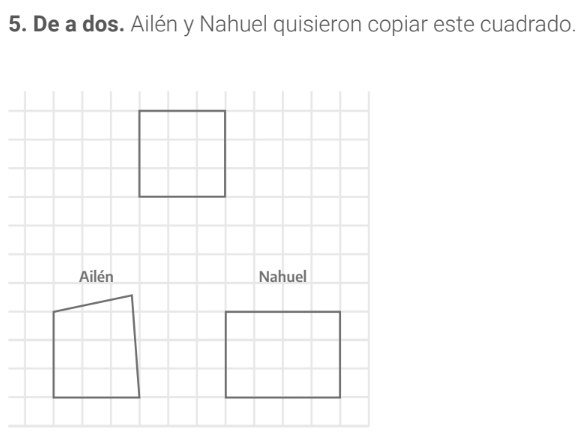
a- ¿En qué les parece que se confundió Ailén?

b- ¿En qué les parece que se confundió Nahuel?

El problema 6 (pág. 11) avanza en la misma dirección. En este caso, se trata de identificar los errores en la copia de un triángulo. Por ejemplo, las y los estudiantes podrán advertir que no coinciden las medidas de los lados, o bien, que “es más achatadito”. Se espera que los intercambios colectivos y las intervenciones de las y los docentes se dirijan a que surjan argumentos como: “el lado sobre el que se apoya el triángulo mide 4 cuadraditos en la original y en la copia también”, “el triángulo original es más alto que la copia”, “hay tres cuadraditos de distancia entre la punta del triángulo y el lado de abajo, en cambio en la copia hay dos”, entre otros posibles. En este problema en particular es posible que una de las dificultades se manifieste al tener que comparar los lados que no coinciden con el cuadriculado de la hoja. En ese caso, es probable que algunas y algunos estudiantes recurran a la regla para medirlos. La o el docente podrá, si lo considera oportuno, destinar un tiempo de la clase para analizar cómo se usa este instrumento y qué problemas permite resolver, dado que probablemente algunas y algunos estudiantes no hayan tenido oportunidad de resolver problemas que involucren su empleo.⁴

Los ítems a- y b- del problema 7 (pág. 11) ofrecen una nueva oportunidad para establecer similitudes y diferencias entre figuras. El nuevo desafío consiste en dejar registro escrito de los rasgos que las identifican. La hoja cuadriculada sigue representando un punto de apoyo para la comparación. En ambos casos se presentan un cuadrado y un rectángulo: las medidas de los lados de cada cuadrado coinciden con las medidas de los lados cortos de cada rectángulo. En el ítem c- se trata de comparar dos triángulos. Para ello las niñas y los niños podrán apoyarse en el cuadriculado y reconocer que la medida de uno de los catetos del primer triángulo coincide con la medida de uno de los catetos del segundo, mientras que los otros catetos son desiguales. Al comparar el tercer lado es probable que identifiquen a simple vista que es “más corto” en el segundo triángulo, o bien, que apelen a la regla para confirmar esa percepción (reinvirtiendo lo discutido a propósito del problema 3).

Para finalizar este apartado, la sección “Para seguir reflexionando y aprendiendo” (pág. 12) apunta a explicitar (sin exigir el uso de vocabulario específico) la igualdad de los lados y la rectitud de los ángulos del cuadrado. La o el docente podrá ampliar la propuesta involucrando otras figuras.

En Más problemas para copiar figuras (pág. 13) se presentan situaciones de copiado de figuras que plantean nuevos desafíos, ya que se incorpora el trazado de diagonales y de figuras “dentro” de otras figuras. Al igual que en los problemas anteriores, la regla se constituye en un recurso que permite trazar líneas rectas para lograr que la copia coincida con la figura original. 

El problema 1 (pág. 13) propone la copia de un rectángulo en hoja cuadriculada, recuperando el tipo de trabajo propuesto en el apartado anterior. En caso de que las y los estudiantes hayan resuelto con comodidad esos problemas, este primer ítem podría obviarse, o bien, ser analizado colectivamente para evocar el trabajo realizado antes de avanzar.

El problema 2 (pág. 13) propone copiar una figura más compleja en la que las niñas y los niños podrían reconocer “dos rectángulos superpuestos” o “un rectángulo dentro de otro”. Esta copia requiere considerar de manera simultánea las características propias de cada rectángulo como así también las distancias entre los lados de ambas figuras (por ejemplo, “este lado del rectángulo chico está un cuadradito más abajo y dos cuadraditos para adentro”).

Es posible que las y los estudiantes copien correctamente cada rectángulo sin conservar la ubicación del rectángulo interior respecto del exterior. Este aspecto podrá revisarse de manera colectiva analizando qué deberían tener en cuenta al volver a intentarlo.

En el problema 3 (págs. 13-14) se propone la copia de distintas figuras en hoja cuadriculada. En el ítem a- se trata de un cuadrado para el que será necesario considerar además de la igualdad de los lados, el trazado de una de sus diagonales. Este trabajo se complejiza en el ítem b-, en el que se han trazado ambas diagonales del cuadrado. El ítem c- plantea el copiado de una figura con características comunes a las anteriores pero que presenta mayores dificultades dado que aparecen más elementos a copiar. Aquí podrían considerar “es un rectángulo de 8 cuadraditos de largo y 4 de ancho” o “son dos cuadrados iguales pegados, de 4 cuadraditos de lado con una diagonal cada uno”. Será interesante poner en diálogo con las y los estudiantes las diferentes formas de mirar la misma construcción. El análisis colectivo a partir de las copias obtenidas será una buena oportunidad para seguir identificando algunas de las características de las figuras geométricas involucradas.

En la sección “Para revisar y resolver” (pág. 14) se propone el intercambio de producciones en parejas para promover la explicitación de los criterios considerados al comparar las figuras originales y las copias.

• Otros problemas para copiar figuras

¿Qué trae de nuevo este apartado respecto del ofrecido en Problemas para copiar y comparar figuras? Tal como mencionamos anteriormente, copiar una figura sobre hoja cuadriculada no reviste la misma complejidad que realizarla sobre hoja lisa. Los problemas que aquí se presentan apuntan a introducir ese nuevo desafío. Será entonces necesario prever la aparición de ciertos errores o desajustes en las primeras producciones, incluso en las de aquellas y aquellos estudiantes que hayan logrado avances significativos en las copias propuestas en apartados anteriores. 

Como ya hemos señalado, el copiado en hoja lisa requiere asumir ciertas decisiones que hasta el momento podían ser resueltas apoyándose en las líneas del cuadriculado. Así, frente al copiado de un rectángulo, las y los estudiantes podían apelar a la cantidad de cuadraditos para determinar la longitud de los lados y “aprovechar” la perpendicularidad y el paralelismo⁵ que ofrece la cuadrícula para que lados y esquinas “queden derechitos”. Estos apoyos desaparecen al usar hoja lisa motorizando así la búsqueda de nuevos modos de obtener la copia solicitada. Es probable que algunas o algunos estudiantes intenten obtener la copia a partir de calcar el dibujo original, es por ello que decidimos restringir esa alternativa explícitamente.

La regla cobra nueva relevancia al constituirse en un recurso para determinar la medida de los lados en lugar de ser usada únicamente para obtener lados rectos. Si bien, en problemas anteriores, las y los estudiantes posiblemente hayan comenzado a emplearla con ese propósito, al copiar en hoja lisa se torna indispensable. En el recuadro “Para recordar y tener en cuenta” (pág. 28) que encabeza el apartado se ofrecen “ayudas” para su utilización.

También es factible que las y los estudiantes recurran a las esquinas de la regla para trazar perpendiculares y ángulos rectos, aún sin usar esos términos. Será entonces interesante sumar el uso de la escuadra a este escenario, dando un tiempo para explorar este nuevo instrumento. Con esta intención, a lo largo del apartado se propone avanzar progresivamente en el análisis de las características de las figuras que podrían reproducirse al usar una escuadra. En el recuadro “Para recordar y tener en cuenta” (pág. 30) se ofrecen algunas pistas para su empleo.

El ítem a- del problema 1 (pág. 29) propone copiar un cuadrado en hoja lisa. Esta tarea implica ensayar estrategias que permitan obtener lados “derechos” e iguales entre sí. Es posible que al intentarlo algunas y algunos estudiantes se apoyen en referencias externas -como por ejemplo, los bordes de la hoja- y que tracen “a ojo” los lados de la figura. Los límites de esta opción podrán ser discutidos en un espacio de trabajo colectivo. El ítem b- busca que las chicas y los chicos se detengan a analizar sus producciones para determinar si quedaron iguales (es decir, que se hagan cargo de validar y justificar su construcción) a la vez que se los invita a explicitar cómo se dieron cuenta. Este trabajo busca colaborar en la explicitación de las características de las figuras que están estudiando (en este caso, del cuadrado). Será interesante retomar las conclusiones registradas al  resolver otros problemas vinculados a las características de las figuras (producidas el mismo año o conservadas de años anteriores) para ampliarlas a partir de las nuevas ideas que van elaborando. 

En la misma dirección, la propuesta para hacer “Entre todas y todos” (pág. 29) apunta a elaborar consejos que ayuden a copiar un cuadrado sobre hoja lisa, valiéndose para ello de nuevos instrumentos. Estos consejos podrán reinvertirse en la propuesta para hacer “De a dos” que invita a intentar una nueva versión de las copias elaboradas en el problema 1. Tal como mencionábamos anteriormente, el recorrido propuesto implica asumir la provisoriedad de las construcciones y dar espacio a la revisión de errores.

• Problemas para ampliar y reducir figuras

Este grupo de problemas enfrenta a las y los estudiantes a un nuevo tipo de tarea: completar el dibujo de una figura en otro tamaño. 

El problema 1 (pág. 15) propone la ampliación de dos figuras sin explicitar en el enunciado de qué figuras se trata. Es probable que algunas y algunos estudiantes analicen las características de las figuras que hay que ampliar antes de emprender la tarea, mientras que otras y otros lo hagan a medida que avanzan en la construcción. En este sentido, el cuadriculado de la hoja será un punto de apoyo para reconocer que el ítem a- presenta un cuadrado (todos sus lados tienen 5 cuadraditos) y que el triángulo del ítem b- tiene dos lados iguales (de 3 cuadraditos cada uno). Ahora bien, a diferencia de los problemas que se incluyen en el apartado Problemas para copiar y comparar figuras, en los que las medidas de original y copia coinciden, en este caso, los lados ampliados del cuadrado y del triángulo miden el doble que los de las figuras originales.

Es importante considerar que, probablemente, las y los estudiantes no adviertan de inmediato que si un lado del cuadrado mide el doble, entonces todos medirán el doble. A su vez, puede resultar aún más complejo advertir que si uno de los lados del triángulo se duplica, los tres lados deberán duplicarse para conservar la forma. Estas relaciones no precisarán ser anticipadas a las y los estudiantes; en cambio, podrán ser analizadas si aparecieran errores de construcción.

En el caso del triángulo del ítem b-, posiblemente, las y los estudiantes consideren que el lado ampliado corresponde a uno de los catetos y continúen el dibujo agregando el otro cateto para luego unir ambos extremos y obtener el tercer lado (hipotenusa)⁶. Será interesante analizar que este último lado también es el doble del de la figura original, esta vez considerando las diagonales de los cuadraditos. 

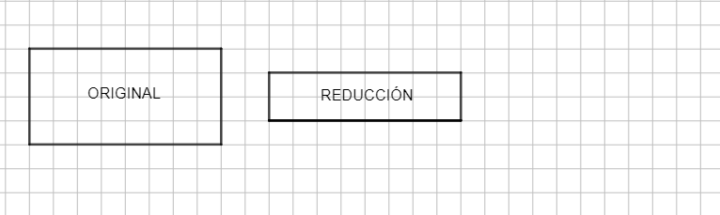
Una tarea semejante se propone en el problema 2 (pág. 19), en este caso se trata de reducir las dimensiones de la figura original de modo que conserve su forma rectangular. Al igual que en el problema 1, las y los estudiantes podrán apoyarse en el cuadriculado para realizar la tarea. Es posible que la reducción del rectángulo les resulte un poco más compleja que la del cuadrado, en el que todos los lados tienen la misma longitud. Aquí deberán considerar la relación que existe entre el lado “corto” de la figura original (4 cuadraditos) y el lado “corto” de la figura reducida (2 cuadraditos) para determinar la longitud de los lados “largos” a completar (“¿será también de 2 cuadraditos menos?”, “¿será la mitad?”). Es posible que para algunas y algunos resulte claro que todos los lados deberán reducirse a la mitad, sin embargo, podría suceder que para otras y otros se trate de quitar 2 cuadraditos a cada lado, tal como sucede con el lado reducido que se ofrece. 

Otro error posible consiste en reducir los lados “cortos” sin modificar los lados “largos”, obteniendo de este modo un rectángulo de la mitad de altura pero del mismo largo tal como se observa en la siguiente imagen:

Una cuestión que es necesario tener en cuenta se vincula con el modo de validar las producciones. En el apartado Problemas para copiar y comparar figuras, dado que original y copia tienen no solo la misma forma sino también las mismas dimensiones, es posible comprobar si ambas coinciden a partir de superponerlas. En cambio, como en este apartado se trata de ampliar o reducir figuras, será preciso poner en diálogo las características de ambas figuras para determinar si se ha logrado agrandar o achicar la figura conservando su forma pues ya no es posible superponerlas para validar la construcción.En la medida en que la o el docente lo crea necesario estas propuestas podrán complementarse con otras más complejas en las que, por ejemplo, se involucre una composición de figuras para agrandar o reducir a partir del cuadriculado de la hoja, tal como se que se propone en la sección “Para revisar y resolver” (pág. 16).

Una vez que hayan finalizado las ampliaciones o reducciones será interesante analizar a qué lados de la figura original corresponden los lados ampliados que se ofrecen. Incluso, este análisis podría realizarse durante la resolución de los problemas que se presentan a lo largo del apartado, por ejemplo, en aquellos casos en que la o el docente advierta que para algunas o algunos estudiantes se torna complejo emprender la tarea de manera autónoma.  

• Problemas para describir figuras 

¿Cuáles son algunos de los desafíos a los que intentamos enfrentar a las y los estudiantes con este tipo de problemas? Las situaciones que se incluyen en este apartado demandan que ellas y ellos interpreten la descripción de una figura determinada, con la intención de que progresen en la explicitación de algunas de sus características y elementos (cantidad de lados, vértices y diagonales; longitud de lados; etc.).

El problema 1 (pág. 17) implica identificar a cuál de las figuras corresponde la descripción que se presenta. Estas relaciones entre figuras y descripciones podrían ponerse en diálogo con el trabajo desplegado en el apartado “Problemas para explorar e identificar figuras”. Las pistas elaboradas y las discusiones en torno a cuáles de ellas caracterizan a una u otra figura y cuáles son comunes a varias de ellas pueden constituirse en insumo para la toma de decisiones en este nuevo problema.  

En el problema 2 (pág. 18) se espera que las y los estudiantes identifiquen la información redundante que se presenta en la descripción que acompaña a la figura. Esta tarea puede resultar costosa dado que las niñas y los niños tienden a agregar detalles de más al describir una figura con la intención de garantizar su claridad, o bien, porque aún están en proceso de aprender la pluralidad de características involucradas en cada término geométrico (por ejemplo, tal vez reconozcan que al decir “es un cuadrado” no precisan aclarar que “tiene 4 lados”, sin embargo, consideran que es necesario decir que tiene cuatro vértices). Será interesante analizar colectivamente qué datos resultan suficientes para describir o identificar una figura.

Para resolver el problema 3 (pág. 18), las y los estudiantes deberán identificar cuál de las dos descripciones corresponde a la figura dada, apoyándose en las características que vienen analizando. Esta tarea se propone para resolver en parejas a fin de propiciar la discusión entre pares. Atendiendo a la diversidad presente en el aula, mientras algunas niñas y algunos niños están trabajando en este problema, la o el docente podrá proponer otras variantes para quienes vayan terminando, por ejemplo, invitar a reescribir las descripciones con distintos propósitos: avanzar en el uso progresivo de vocabulario específico (“¿de qué otra manera podríamos haber indicado que tiene dibujada una línea que va de un vértice al vértice opuesto?” ), o bien, analizar si las descripciones presentan información redundante (“¿será necesario decir, cuando se traza la diagonal de un rectángulo, que quedan conformados dos triángulos?”).

• Instrucciones para construir figuras

Los problemas propuestos en este apartado tienen la intención de avanzar en la interpretación y la elaboración de instructivos para construir figuras como medio para  profundizar el estudio de sus características.

El problema 1 (pág. 19) solicita la construcción de una figura a partir de un instructivo.

Se trata de un cuadrado al que se le ha trazado una base media⁷(una línea que va desde la mitad de uno de los lados hasta la mitad del lado opuesto). Es probable que las y los estudiantes obtengan dibujos como estos:

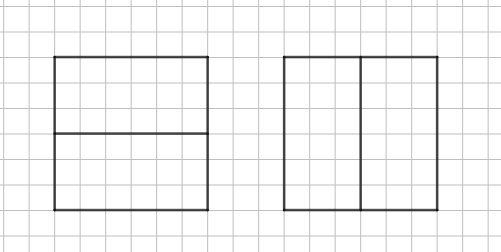
En un espacio de trabajo colectivo será interesante discutir si se trata de dos construcciones posibles para el mismo instructivo o si es la misma figura en otra posición. Para dirimir esta cuestión, podrán superponerlas y advertir que coinciden, es decir, que representan la misma figura. Es por ello que será conveniente que realicen las construcciones en hoja aparte de modo de realizar la superposición a trasluz con comodidad.

En el problema 2 (págs. 19-20), las y los estudiantes deberán elaborar instructivos que permitan construir las figuras propuestas: un cuadrado en a- y un rectángulo en b-, en ambas casos con sus dos diagonales. Puede ser una instancia fértil para retomar y ampliar las ideas elaboradas hasta el momento en torno a  “distintas maneras de decir lo mismo”, la información que pueda resultar redundante y el uso progresivo de un vocabulario cada vez más ajustado. Por ejemplo, en lugar de “trazar una línea que va de un vértice al opuesto” apelar a “diagonal”.

El ítem a- del problema 3 (pág. 20) propone establecer relaciones entre un instructivo y dos interpretaciones posibles. En un espacio de trabajo colectivo podrá discutirse si se trata de un error de quien reproduce la figura a partir del mensaje o si el mensaje es confuso o ambiguo. Se apunta a que las y los estudiantes identifiquen que es posible dibujar cualquiera de las dos figuras con esas instrucciones. El ítem b- agrega la posibilidad de reformular el mensaje de modo que dé lugar a la construcción de una única figura.

 El problema 4 (pág. 21) involucra la elaboración de un instructivo de una figura más compleja: un rectángulo en el que se trazaron una diagonal y una base media. Será importante tener en cuenta el análisis realizado a partir de los problemas anteriores de modo de lograr un instructivo que permita dibujar esa figura sin confusiones ni información redundante. Por ejemplo, ¿cómo indicar con claridad cuál de las dos bases medias trazar? 

La sección “Para seguir reflexionando y aprendiendo” permite recapitular lo trabajado hasta el momento y revisitar los problemas incluidos en este apartado para sistematizar algunos conocimientos.

• Figuras usando otras figuras

Este conjunto de problemas apunta a que las y los estudiantes avancen en el análisis de las relaciones entre triángulos y cuadrados, entre triángulos y rectángulos y entre cuadrados y rectángulos. En esta ocasión, la exploración de relaciones entre figuras se provoca a partir de los sucesivos intentos de cubrir completamente una figura usando otras, o bien, la determinación anticipada de la cantidad de figuras que serán necesarias para lograrlo. 

Es importante mencionar que el tipo y cantidad de figuras que se proponen para cubrir otras se constituyen en variables didácticas que la o el docente podrá comandar para modificar la complejidad de los problemas en función de los conocimientos de sus estudiantes. A su vez, tal como hemos planteado anteriormente, podrían proponerse diversos problemas en forma simultánea en una misma clase, sea de sección única o plurigrado, preservando que todas y todos tengan oportunidad de compartir sus ideas y las de sus compañeras y compañeros en espacios de trabajo grupal o colectivo.

Al avanzar en los problemas, las y los estudiantes precisarán detenerse en las particularidades de cada figura (cantidad de vértices, cantidad y longitud de los lados) y tomar decisiones acerca de cuántas veces entra una figura en otra. Esto requerirá analizar también en qué posición convendría ubicarlas para evitar superposiciones o espacios sin cubrir.

En el problema 1 (pág. 23) se propone hallar la cantidad de cuadrados (A) que se necesitan para cubrir otro mayor (B). En este caso las figuras solo se diferencian por su tamaño por lo que el problema radicará en anticipar la posición en la que deberían colocarse los cuadrados pequeños para que cubran el grande respetando la condición solicitada. Para determinar que el cuadrado grande puede cubrirse con 4 cuadrados pequeños, las chicas y los chicos podrían hacer marcas en el cuadrado B, o bien, dibujar en otra hoja varios cuadrados A para cubrir efectivamente el cuadrado B. Esta estrategia podría habilitarse incluso para validar sus anticipaciones.

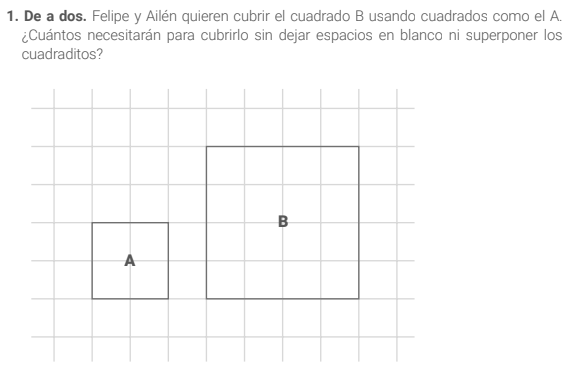
En el problema 2 (pág. 24), las chicas y los chicos deberán determinar si es cierto que con tres cuadrados iguales al dado se cubre el rectángulo que se ofrece. Aquí, a diferencia del problema anterior, entra en juego la idea de que repitiendo una figura se puede formar otra diferente, no solo en su tamaño sino también en su forma. Será interesante habilitar un espacio de intercambio en el que comiencen a explicitar por qué alcanzan dos cuadrados iguales al dado para cubrir este rectángulo. Si la o el docente lo considera pertinente, también será posible introducir nuevas preguntas que podrían plantearse a toda la clase o a un grupo de estudiantes: ¿todos los rectángulos podrían ser cubiertos por dos cuadrados iguales?, y si no alcanzara con dos, ¿podría decirse que cualquier rectángulo puede cubrirse con tres o más cuadrados iguales?  

En los problemas 3 y 4 (págs. 24-25), las niñas y los niños se enfrentan a dos nuevos desafíos: anticipar qué características tendrá la figura buscada y trazarla de modo que se sostengan dichas características. Si bien desde ambas consignas se solicita el trazado de una única figura, en un espacio de trabajo colectivo, al advertir que las compañeras y los compañeros encontraron otras figuras posibles, será interesante promover la discusión  acerca de la cantidad de soluciones que admiten estos problemas.

Los problemas 5 a 7 (págs. 25-27) avanzan en el establecimiento de relaciones entre figuras. Esta vez, se utilizan triángulos para cubrir cuadrados y rectángulos. El problema 5 vuelve a proponer que decidan si están de acuerdo o no con la afirmación de otro estudiante. Frente a las respuestas afirmativas será interesante analizar con la clase en qué posición (o en qué posiciones) podrán ubicarse los triángulos para cubrir este cuadrado. Es probable que, durante el intercambio, algunas o algunos estudiantes adviertan que “hay que hacer coincidir las puntas”. Los problemas 6 y 7 permiten reinvertir las relaciones analizadas en los problemas anteriores. Por ejemplo, podrán colocar cuadrados uno al lado del otro y obtener distintos rectángulos.

En la sección Para revisar y resolver se recuperan los problemas 2, 3, 4 y 7 con la intención de profundizar el análisis acerca de la cantidad de soluciones posibles.

En este documento hemos intentado acompañar el análisis de los problemas del material para estudiantes. Esperamos que su lectura constituya un aporte para la planificación y la gestión de las clases.

---

¹ Resulta interesante distinguir dibujo y figura. El dibujo es la representación de una figura, en tanto que la figura es un objeto “ideal” que puede caracterizarse por un conjunto de relaciones.

² Este juego también podrá proponerse en Segundo Ciclo, por ejemplo, a partir de una colección de triángulos variados para introducir la clasificación por sus lados y sus ángulos (dado que todas las figuras tienen tres lados, será necesario recurrir a la longitud de los lados o a la amplitud de los ángulos para distinguirlas).

³ Al finalizar el material para estudiantes encontrarán hojas con cuadriculado de distintos tamaños para las construcciones de figuras que se solicitan en cada problema. En el caso del copiado, el hecho de realizarlas en otra hoja habilitará la superposición con el original para comprobar si coinciden. 

⁴ Podrán encontrar propuestas vinculadas al uso de este instrumento en “Actividades para continuar estudiando, Cuadernillo de actividades para la continuidad pedagógica,Tercer año, Quinta entrega”.

⁵ Estos conceptos serán abordados de manera explícita en Segundo Ciclo, sin embargo, de manera implícita, las y los estudiantes comienzan a reparar en la necesidad de considerar ambas condiciones, incluso llegando a elaborar algunas formulaciones provisorias (“estos dos lados tienen que quedar derechitos”, “estos dos lados están torcidos, se van a cruzar”, etc.) que podrán convivir junto a otras más precisas hasta que sean retomadas y profundizadas más adelante.

⁶ Reiteramos que no se espera que estos términos (cateto e hipotenusa) sean utilizados por las y los estudiantes en Primer Ciclo.

⁷ Es importante aclarar que el uso de este término está dirigido al lector pero no se propone para las y los estudiantes.