Procesamiento de datos agrometeorológicos con Excel
Secuencia didáctica orientada a procesar grandes volúmenes de datos generados por el INTA utilizando Excel.
Creado: 18 junio, 2024 | Actualizado: 23 de mayo, 2025
Autoría:
Sentido de la secuencia didáctica
Por medio de esta propuesta se busca que las y los estudiantes aprendan a manejar datos reales, utilizando para su explicación datos provenientes de la unidad meteorológica de Estación Experimental Agropecuaria del INTA Rafaela. Se propone el desarrollo de habilidades en el uso de herramientas estadísticas básicas para interpretar y analizar la información. Esto les permitirá comprender mejor los fenómenos climáticos y su impacto en la agricultura, así como también desarrollar competencias técnicas y analíticas valiosas para su formación profesional.
Los objetivos pedagógicos de esta secuencia son, entre otros, los siguientes:
- Desarrollar habilidades en el uso de Excel para procesar y analizar datos agrometeorológicos.
- Comprender y aplicar conceptos de estadística descriptiva, como promedio, desvío estándar y distribución normal.
- Interpretar y analizar datos meteorológicos para obtener perfiles agrometeorológicos regionales.
- Fomentar el trabajo en equipo y la presentación oral de resultados técnicos.
- Promover el uso de datos reales y actuales en la toma de decisiones agronómicas.
Primer momento. Actividad inicial
El objetivo de esta primera instancia es relevar los conocimientos previos de las y los estudiantes sobre el tema, para luego introducir al grupo en el trabajo con datos. Para ello, se proponen diferentes actividades.
Discusión en clase
- Preguntar a las y los estudiantes qué saben sobre la obtención y el significado de promedio y desvío estándar.
- Introducir el concepto de distribución normal y su importancia en el análisis de datos.
- Explicar cómo se puede utilizar Excel para procesar grandes volúmenes de datos.
Ejercicio práctico
- Proporcionar un conjunto pequeño de datos y pedir a las y los estudiantes que calculen manualmente el promedio y el desvío estándar (utilizar para esto mediciones realizadas en el entorno formativo). Por ejemplo, en la huerta medir el área de las hojas de lechuga o el peso de los lechones nacidos, entre otras posibilidades de registro de variables medidas en el entorno.
- Comparar los resultados manuales con los obtenidos al utilizar las funciones de Excel.
Segundo momento. Definición y utilidad práctica de las medidas de tendencia central
Promedio (Media)
El promedio, o media aritmética, es el valor que se obtiene al sumar todos los datos de un conjunto y dividir el resultado entre la cantidad total de datos.
Es útil para encontrar el valor representativo de un conjunto de datos. Se utiliza en una amplia variedad de campos, como la economía, la educación y la meteorología, para proporcionar una visión general de un conjunto de datos. Por ejemplo, en meteorología, el promedio de las temperaturas diarias de un mes puede ayudar a entender el clima típico de ese período.
Moda
La moda es el valor que con más frecuencia aparece en un conjunto de datos.
Es útil para identificar el valor más común o habitual en el conjunto de datos. Esto puede ser especialmente útil en contextos donde la frecuencia de ocurrencia es importante. En meteorología, por ejemplo, la moda de las temperaturas máximas diarias puede indicar la temperatura más común durante un mes.
Mediana
La mediana es el valor central en un conjunto de datos ordenados. Si el número de observaciones es impar, es el valor del medio. Si es par, es el promedio de los dos valores centrales.
Es útil porque no se ve afectada por valores extremadamente altos o bajos (outliers). Proporciona una medida de tendencia central que representa mejor un conjunto de datos con valores atípicos. Por ejemplo, la mediana de las precipitaciones diarias puede ofrecer una visión más precisa de las condiciones típicas de lluvia en una región con eventos de lluvia extremos.
Sentido de calcular el desvío estándar
El desvío estándar es una medida de dispersión que indica cuánto se desvían los valores de un conjunto de datos respecto al promedio.
Es crucial para comprender la variabilidad de los datos. Si es bajo, indica que los datos están agrupados cerca del promedio, mientras que un desvío estándar alto indica una mayor dispersión.
El desvío estándar puede usarse en función de:
Evaluación de la consistencia. En meteorología, un bajo desvío estándar de las temperaturas diarias sugiere un clima más consistente, mientras que un alto desvío estándar indica mayor variabilidad.
Comparación de variabilidad. Permite comparar la variabilidad entre diferentes conjuntos de datos. Por ejemplo, de las precipitaciones entre dos regiones.
Toma de decisiones. Ayuda en la toma de decisiones basadas en la comprensión de la variabilidad de los datos. En la agricultura, conocer la variabilidad de la precipitación puede influir en las decisiones sobre el riego y la gestión del cultivo.
Por qué son medidas de tendencia central
Las medidas de tendencia central son valores que intentan describir un conjunto de datos mediante un valor representativo. Son fundamentales por lo que se explica a continuación.
Promedio: proporciona una visión general del conjunto de datos.
Moda: indica el valor más común, útil para entender qué es lo más frecuente.
Mediana: ofrece una medida central que no se ve afectada por valores extremos, ideal para distribuciones sesgadas.
En conjunto, estas medidas permiten a analistas, científicas y científicos resumir y entender grandes volúmenes de datos de manera efectiva, y proporcionar información clave que puede guiar decisiones y acciones.
Cálculo y ejemplos para practicar antes de trabajar en Excel
Se recomienda recuperar valores medidos de otras variables extraídas del entorno formativo de la escuela para ampliar las posibilidades y los ejemplos de cálculo y aplicación de estos conceptos.
Promedio
Es el valor central de un conjunto de datos. Se calcula sumando todos los valores y dividiéndolos por la cantidad de valores.
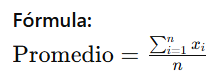
Ejemplo meteorológico: si se dispone de las temperaturas máximas diarias de una semana:
- Lunes: 25°C
- Martes: 27°C
- Miércoles: 26°C
- Jueves: 28°C
- Viernes: 24°C
- Sábado: 27°C
- Domingo: 26°C
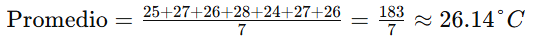
Desvío estándar
El desvío estándar mide la dispersión de un conjunto de datos respecto al promedio. Indica cuánto se desvían los valores respecto a la media.
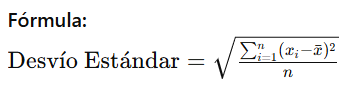
Ejemplo meteorológico: Utilizando las mismas temperaturas máximas, primero se calculan las diferencias respecto del promedio y luego la varianza.

Tercer momento. Distribución normal
Es una distribución de probabilidad continua, simétrica respecto a su media, donde los valores cercanos a la media son más frecuentes.
Ejemplo meteorológico: si las temperaturas diarias de un mes siguen una distribución normal, la mayoría de los días tendrán temperaturas cercanas al promedio mensual, y muy pocos días tendrán temperaturas extremadamente altas o bajas.
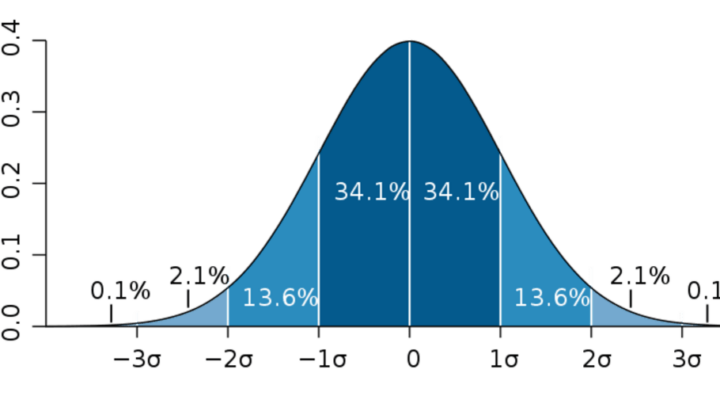
Una distribución normal, también conocida como distribución de Gauss o campana de Gauss, es una de las distribuciones de probabilidad más importantes en estadística. Aquí se describen sus características y se presenta una explicación de su gráfica.
Características de la distribución normal
Forma de campana. La gráfica de una distribución normal tiene una forma de campana simétrica alrededor de su media.
Media, mediana y moda. En una distribución normal, la media, la mediana y la moda coinciden en el mismo punto, que es el centro de la distribución.
Simetría. Es perfectamente simétrica respecto a su media, lo que significa que el lado izquierdo de la media es una imagen especular del lado derecho.
Asintótica. La curva se aproxima al eje horizontal pero nunca lo toca, extendiéndose indefinidamente en ambas direcciones.
Desviación estándar. La forma de la distribución está determinada por su desviación estándar. Una desviación estándar mayor resultará en una curva más ancha y baja, mientras que una desviación estándar menor resultará en una curva más estrecha y alta.
Regla empírica (68-95-99.7)
- Aproximadamente el 68% de los datos caen dentro de una desviación estándar de la media.
- Aproximadamente el 95% de los datos caen dentro de dos desviaciones estándar de la media.
- Aproximadamente el 99.7% de los datos caen dentro de tres desviaciones estándar de la media.
Gráfica de la distribución normal
La gráfica de una distribución normal es una curva suave y continua en forma de campana. A continuación, se presenta un ejemplo de cómo es una distribución normal estándar (con media 0 y desviación estándar 1).
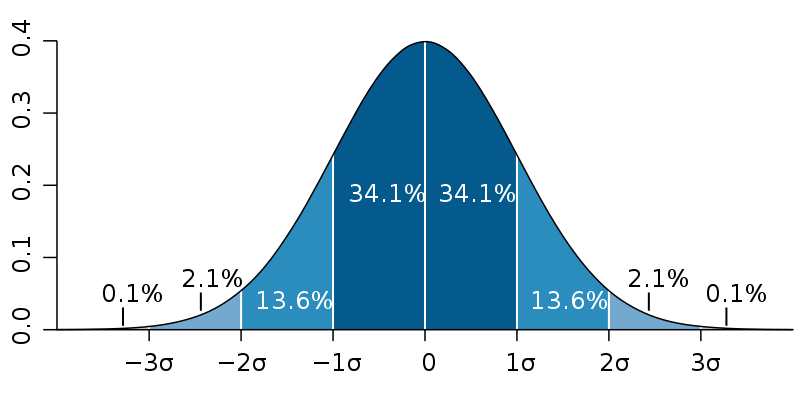
Archivo DGCyE.
La distribución normal tiene varias aplicaciones importantes en el análisis de variables agropecuarias. A continuación, se presentan algunas de las formas en las que se utiliza.
Aplicaciones de la distribución normal en el análisis de variables agropecuarias
Las aplicaciones de distribución normal pueden utilizarse con distintas finalidades. A continuación se describen algunas.
Modelado de rendimientos de cultivos
- Estimación de rendimientos. Se pueden utilizar distribuciones normales para modelar los rendimientos de cultivos bajo condiciones normales, permitiendo la estimación de promedios y variabilidad.
- Evaluación de riesgos. La distribución normal ayuda a evaluar la probabilidad de obtener rendimientos dentro de ciertos rangos, lo cual es esencial para la gestión del riesgo agrícola.
Control de calidad en la producción
- Control de procesos. Las personas dedicadas a la producción pueden usar la distribución normal para monitorear y controlar la calidad de productos agrícolas, como el tamaño y peso de los frutos, asegurándose de que cumplan con los estándares establecidos.
- Detección de anomalías. Al comparar los datos recolectados con una distribución normal esperada, es posible detectar desviaciones significativas que indiquen problemas en la producción o en las prácticas de manejo.
Estudios de experimentación agrícola
- Diseño de experimentos. En la investigación se pueden usar distribuciones normales para diseñar experimentos agrícolas, y analizar los efectos de diferentes tratamientos sobre los cultivos.
- Análisis estadístico. Los resultados de los experimentos pueden ser analizados a partir de la utilización de pruebas estadísticas que asumen una distribución normal, como la prueba t y el ANOVA1, para determinar la significancia de los efectos observados.
Pronóstico y simulación de variables climáticas
- Modelado climático. Las variables climáticas, como la temperatura y las precipitaciones, a menudo se asumen normalmente distribuidas para fines de modelado y pronóstico; esto ayuda a planificar las actividades agrícolas.
- Análisis de riesgo climático. Evaluar la probabilidad de eventos extremos (como heladas o sequías) mediante la distribución normal permite tomar decisiones informadas sobre prácticas de mitigación y adaptación en la agricultura.
Optimización de recursos
- Asignación de recursos. La distribución normal puede utilizarse para modelar la demanda y oferta de recursos agrícolas, optimizando su asignación para maximizar la eficiencia y minimizar los costos.
- Planeación de cosechas. Permite prever las fluctuaciones en la producción y ajustar la planificación de las cosechas para asegurar una oferta continua y estable.
Cuarto momento. Visualización y análisis de datos
La visualización de datos agropecuarios en forma de gráficos de distribución normal puede proporcionar una comprensión clara de la variabilidad y la tendencia central de las variables medidas, como el peso de los granos, el contenido de humedad o la producción de leche en vacas.
Resumen de características
Forma de campana. La simetría y la forma específica ayudan a identificar patrones de comportamiento típicos.
Media, mediana y moda coincidentes. Facilita la interpretación de los datos, ya que un solo valor central resume la tendencia central.
Simetría y asintoticidad. Proveen un marco para entender la dispersión de los datos y la probabilidad de valores extremos.
Desviación estándar. Permite evaluar la dispersión de los datos respecto a la media, lo cual es crucial para tomar decisiones informadas en la gestión agropecuaria.
El uso de la distribución normal en el análisis de variables agropecuarias proporciona una base estadística robusta para la toma de decisiones, al tiempo que mejora la precisión y eficiencia en la gestión agrícola.
Moda
La moda es el valor que más se repite en un conjunto de datos.
Ejemplo meteorológico: si en un mes se registran las siguientes temperaturas máximas diarias (25, 26, 27, 25, 28, 25, 27, 25, 26, 27, 25, 28, 25, 27) la moda sería 25°C, ya que es la temperatura que más veces se repite (valor más frecuente).
Mediana
La mediana es el valor central de un conjunto de datos ordenados. Si hay un número par de valores, se toma el promedio de los dos valores centrales.
Ejemplo meteorológico: para las temperaturas máximas diarias (24, 25, 25, 26, 27, 27, 28, 24, 25, 25, 26, 27, 27, 28) la mediana es 26°C, ya que es el valor central del conjunto ordenado.
Quinto momento. Proceso en Excel
A continuación se ejemplifica cómo trasladar a Excel los conceptos abordados en el punto anterior, utilizando datos meteorológicos.
Promedio: usar la función =PROMEDIO(A1:A7) para calcular el promedio de las temperaturas máximas.
Desvío estándar: usar la función =DESVEST(A1:A7) para calcular el desvío estándar.
Moda: usar la función =MODO(A1:A7) para encontrar la moda.
Mediana: usar la función =MEDIANA(A1:A7) para encontrar la mediana.
Sexto momento. Descarga y procesamiento de datos
En este momento se propone que las y los estudiantes puedan realizar una simulación de procesamiento de datos meteorológicos de una unidad específica. En este caso se trata de la Estación Experimental Agropecuaria del INTA Rafaela.
Objetivo: descargar y procesar los datos agrometeorológicos de la unidad meteorológica EEA INTA Rafaela.
Explicación del procedimiento
- Descarga de datos. Se realizará un ejercicio práctico de cómo acceder a los datos públicos disponibles desde el sitio web del Sistema de Información y Gestión Agrometeorológica del INTA.
- Importación y preparación de los datos en Excel. Se enseñará a importar a Excel los archivos de datos obtenidos desde el sitio web en formato CSV; y posteriormente cómo insertar una tabla para organizar dichos datos.
Análisis de datos
- Se introducirá en la creación de tablas dinámicas para cada una de las variables en estudio: precipitaciones; temperaturas medias, mínimas y máximas; y humedad relativa media.
- Se abordará la representación gráfica de las distribuciones de estas variables, por ejemplo, las precipitaciones por mes en cada año de la serie.
Paso 1. Para iniciar el ejercicio práctico, se ingresa al Sistema de información y Gestión Agrometeorológica desde donde será posible acceder a las estaciones meteorológicas en línea.
Para ello, se van a dejar activas solo las unidades meteorológicas en línea de INTA (verdes).
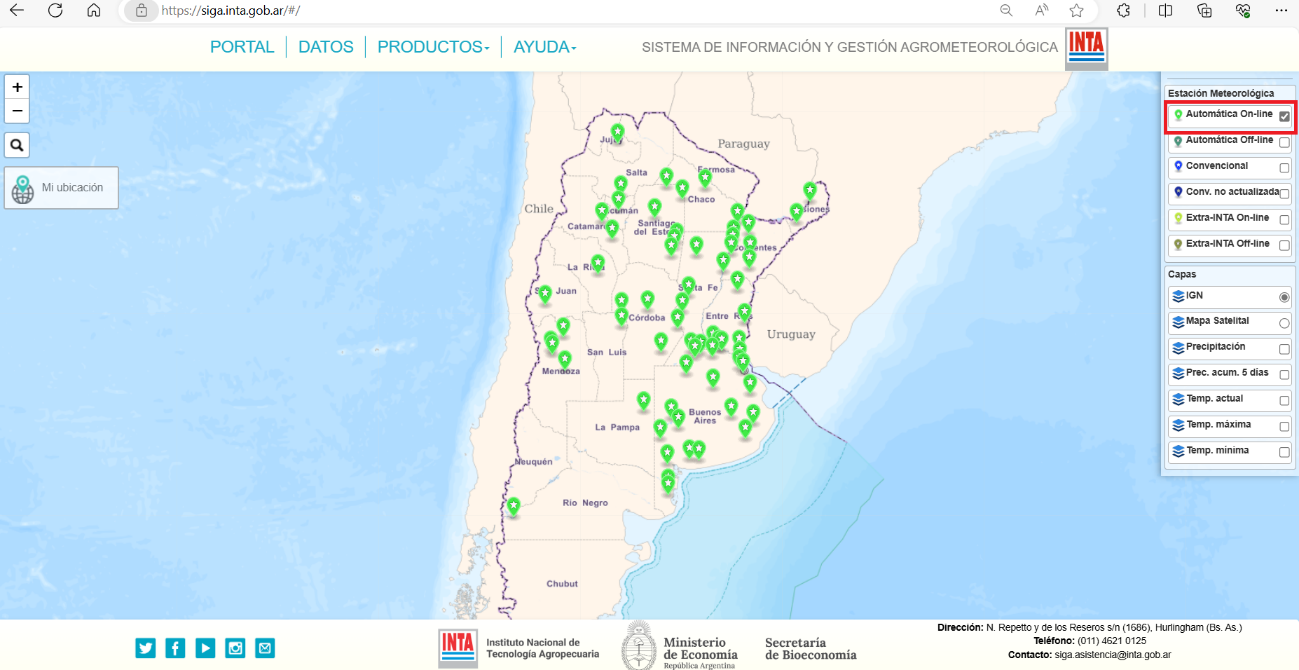
Paso 2. Se selecciona en la unidad meteorológica elegida, en el ejemplo Rafaela INTA.
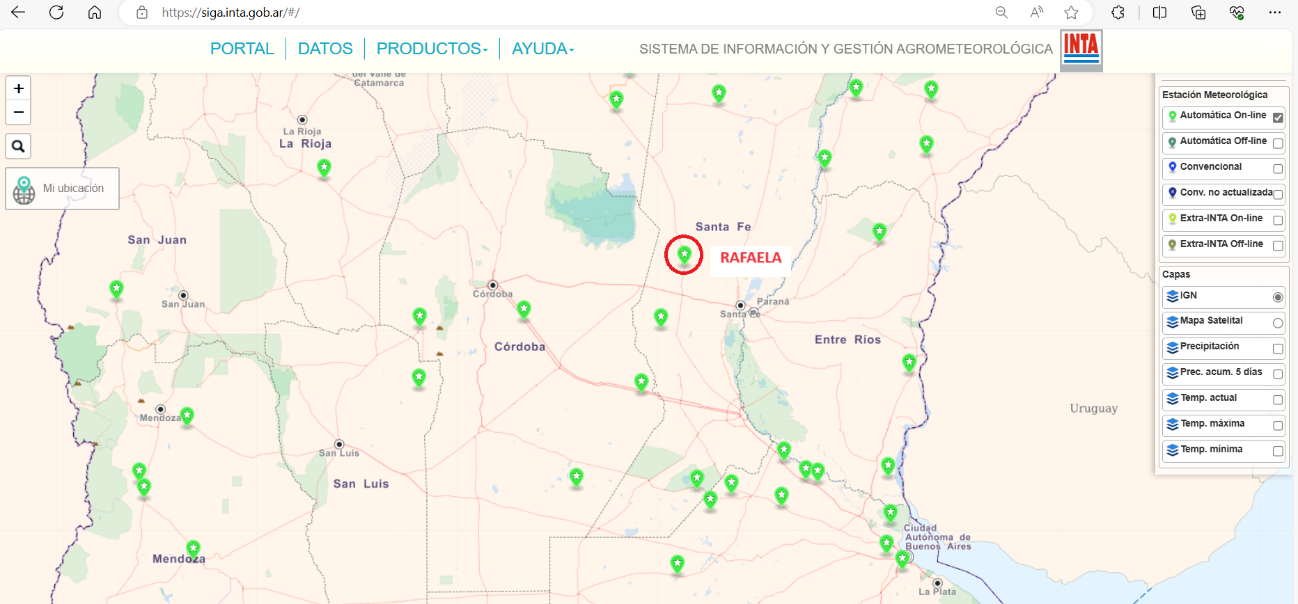
Paso 3. Seleccionar la opción Más Datos.
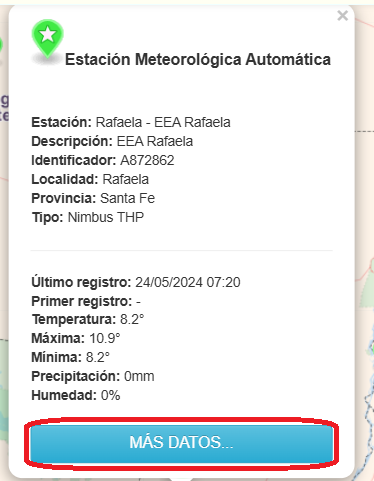
Paso 4. Hacer clic en Búsqueda avanzada.
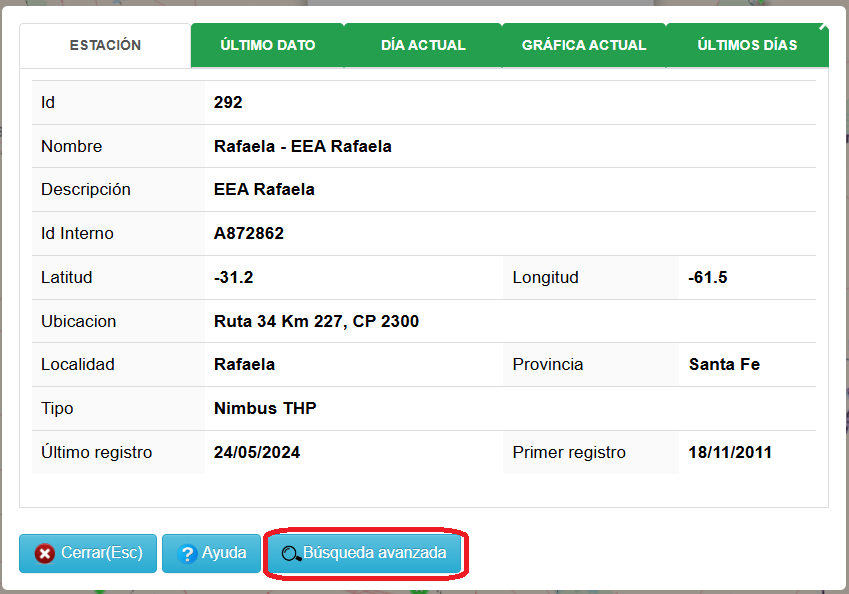
Paso 5. Hacer clic en Descargar para obtener el archivo con los datos históricos de la Unidad Meteorológica.
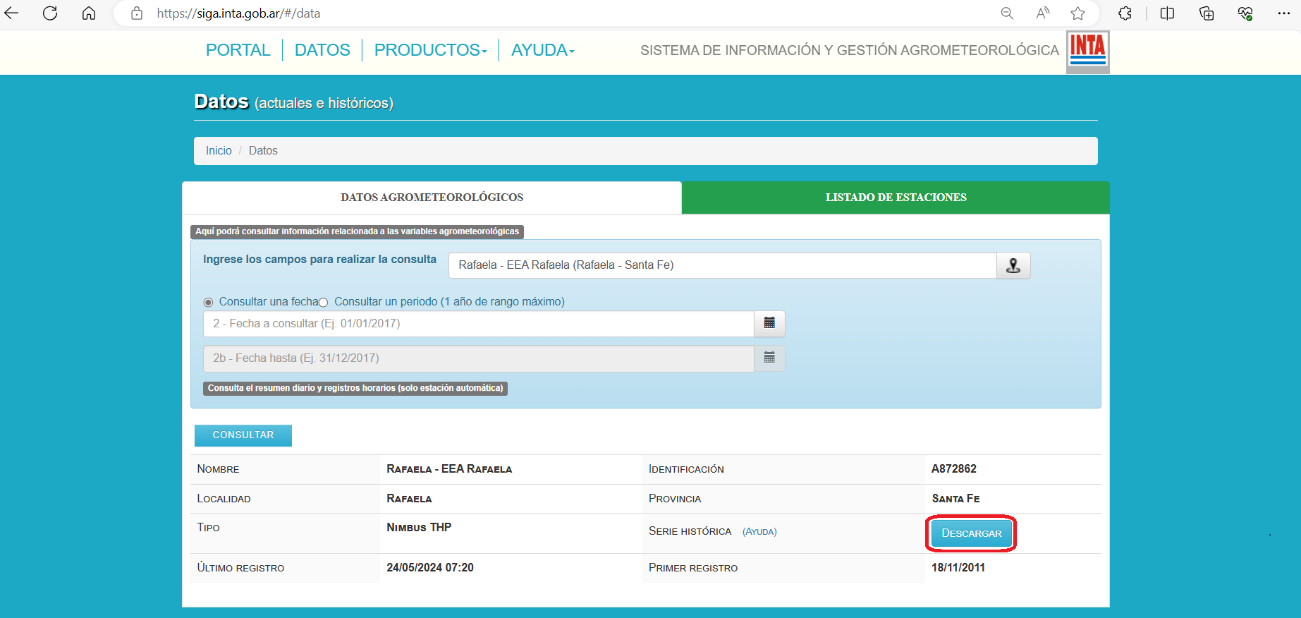
Luego de descargar el archivo es necesario editar los datos, ya que su formato es texto y hay que transformarlos a valores numéricos que permitan luego realizar cálculos.
Con el archivo abierto, seleccionar las columnas (de a una) que están a la derecha de la columna fecha (A), y transformar los datos columna a columna.
El procedimiento es:
- Seleccionar la columna haciendo clic en la letra, ejemplo la columna D.
- Ir a Menú principal (cinta de comandos principal) Datos > Texto en columnas > seguir los tres pasos de la transformación:
Paso 1 de 3:
Paso 2 de 3:
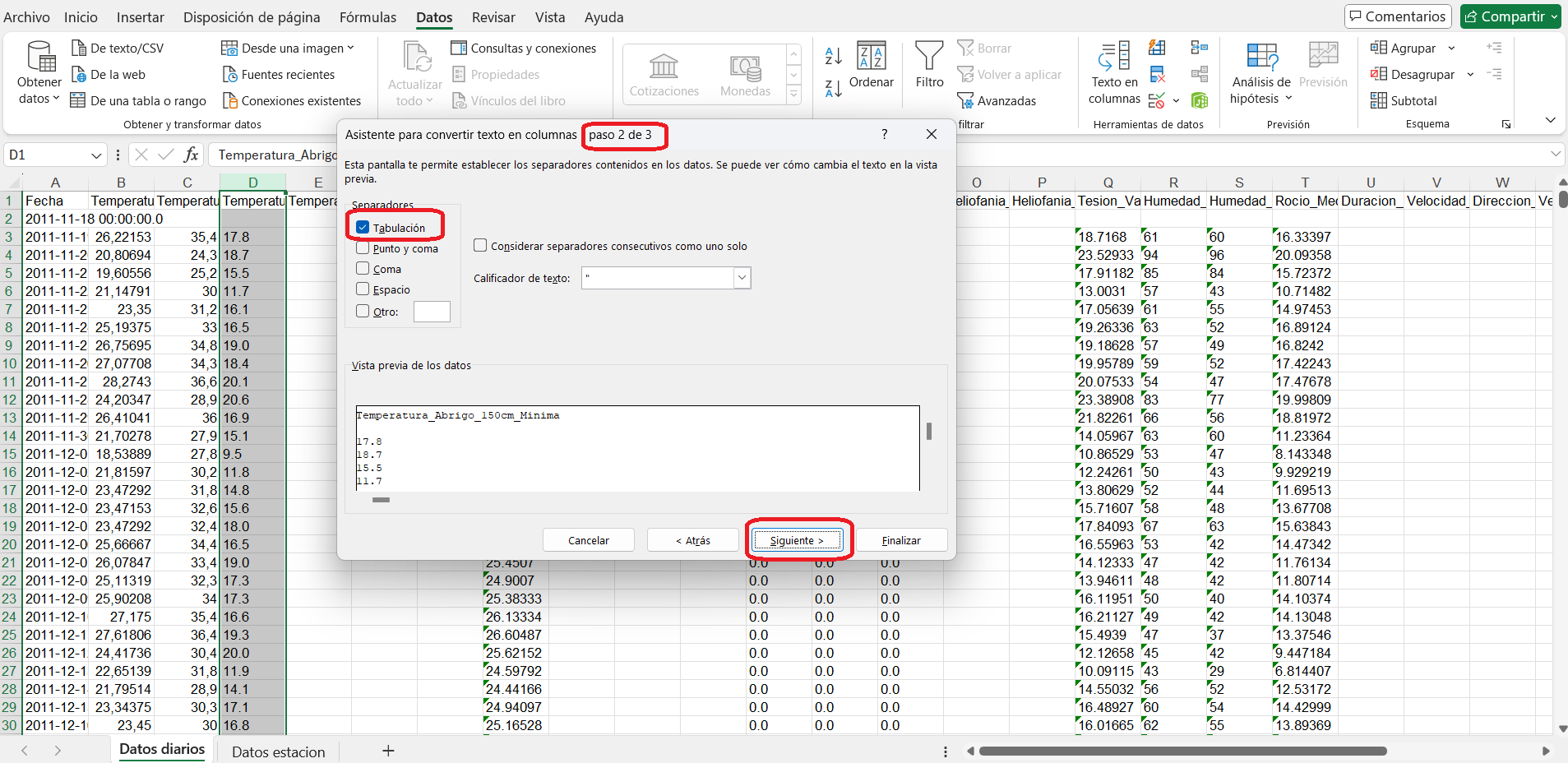
Paso 3 de 3: hacer clic en avanzadas.
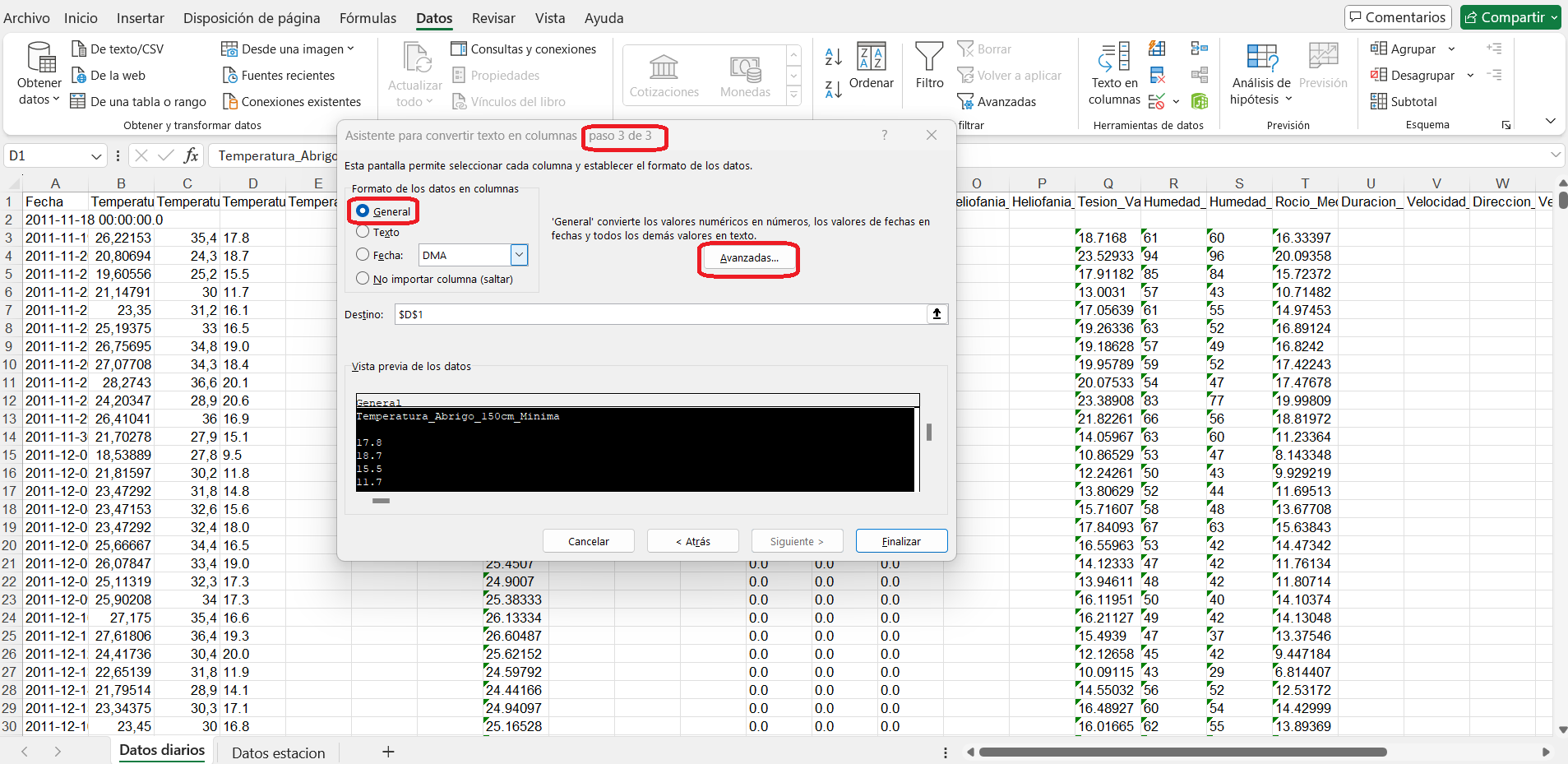
Paso 3 de 3: cambiar los símbolos coma y punto, y aceptar.
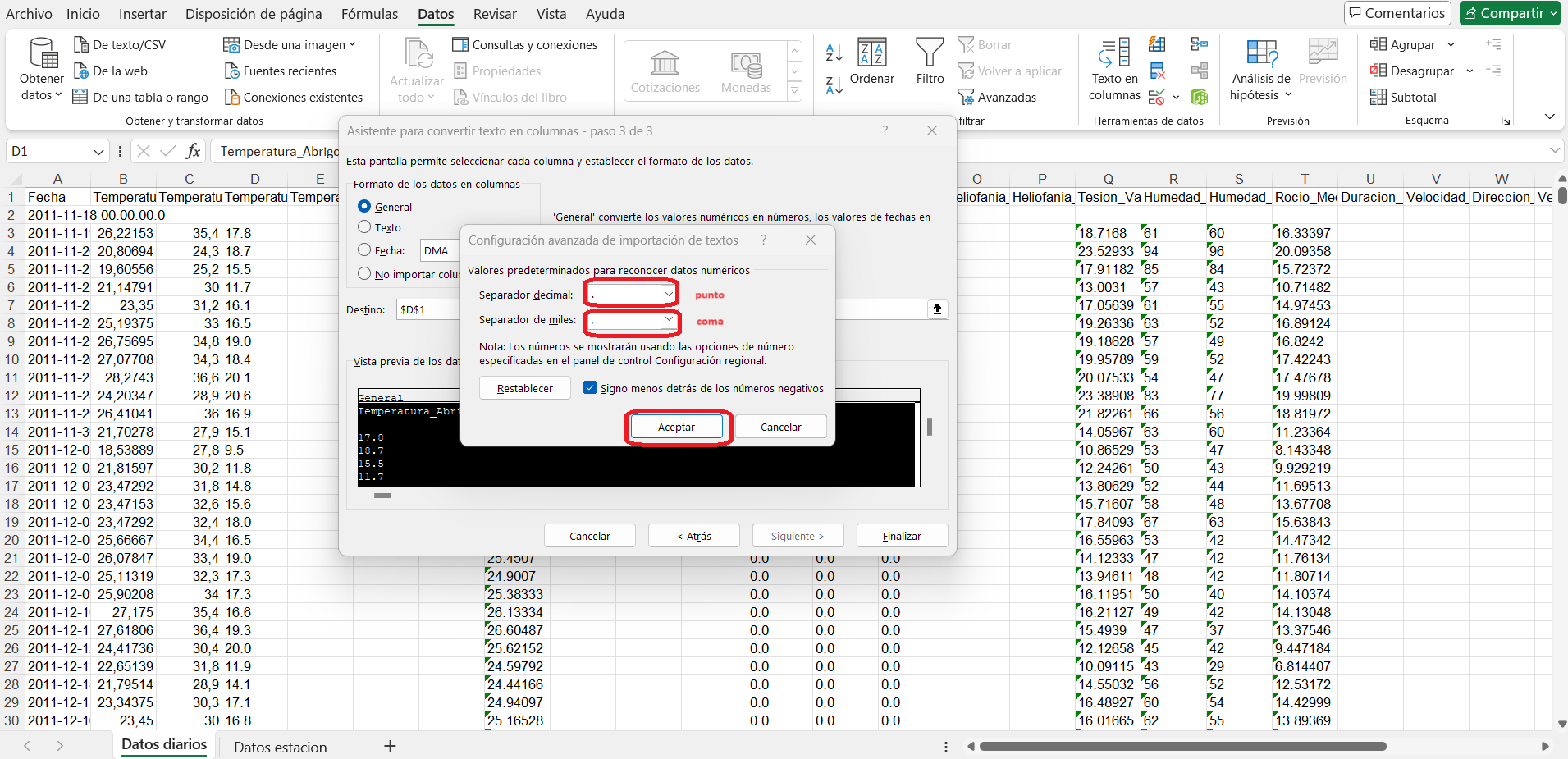
Este procedimiento se realiza en todas las columnas con datos.
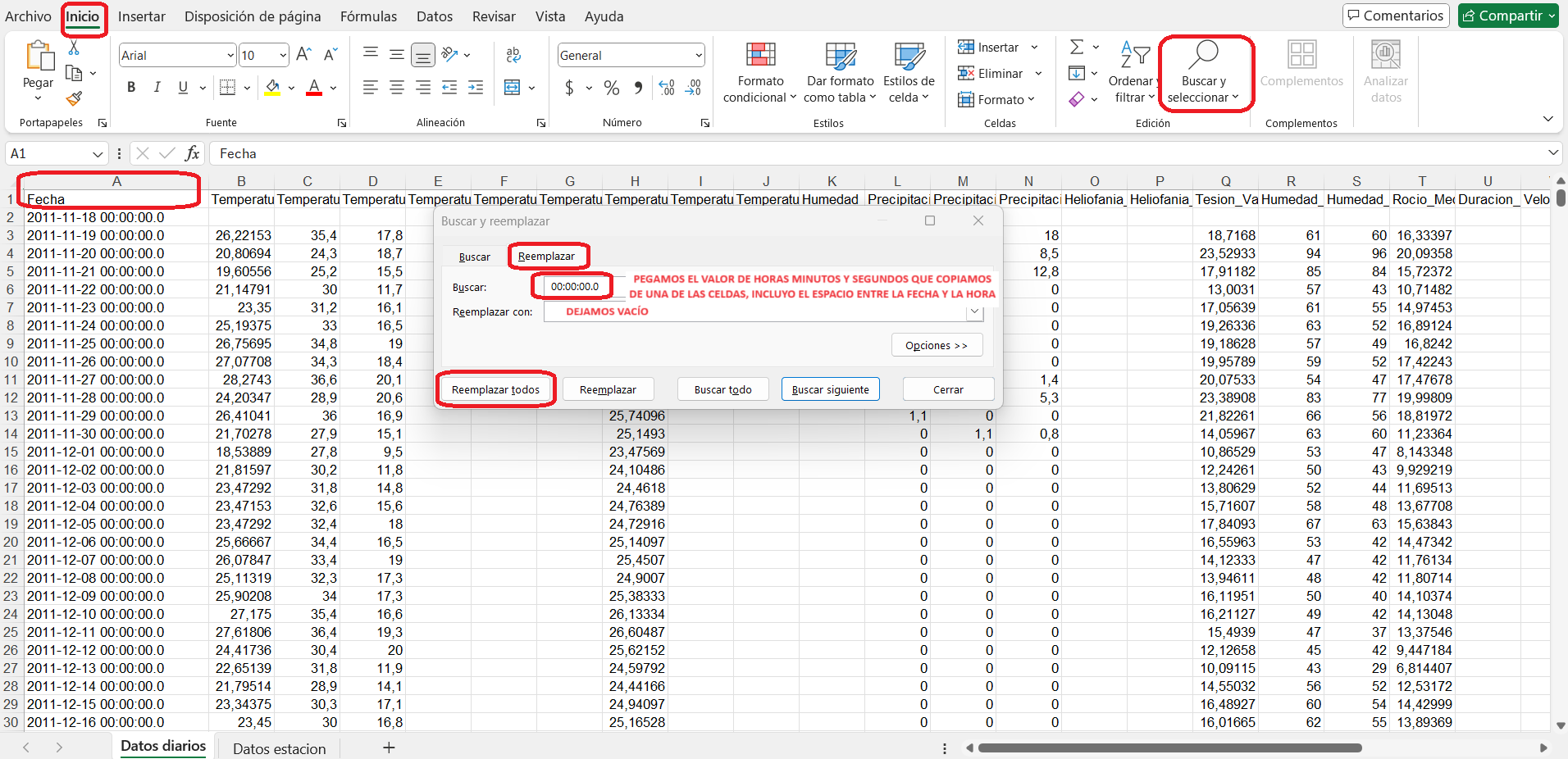
Para finalizar, se modifica la columna “Fecha” (A), se reemplaza el dato de horas, minutos y segundos de la unidad meteorológica para dejar solo la fecha. Al hacerlo, copiar de la primera celda (A2) el valor y el espacio delante del valor, para reemplazarlo en todas las celdas.
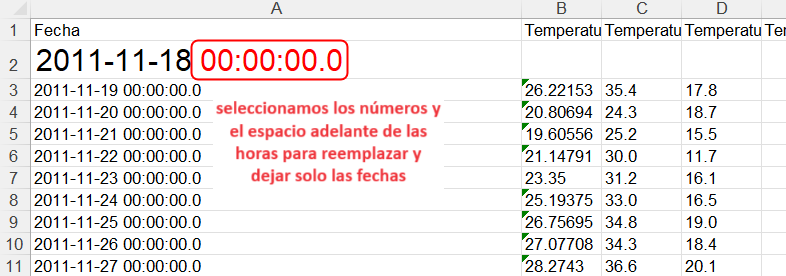
Para hacer el cambio, ir a Inicio > Buscar y seleccionar > Reemplazar > Pegar en el campo.
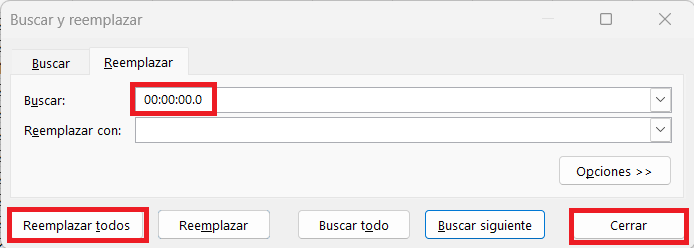
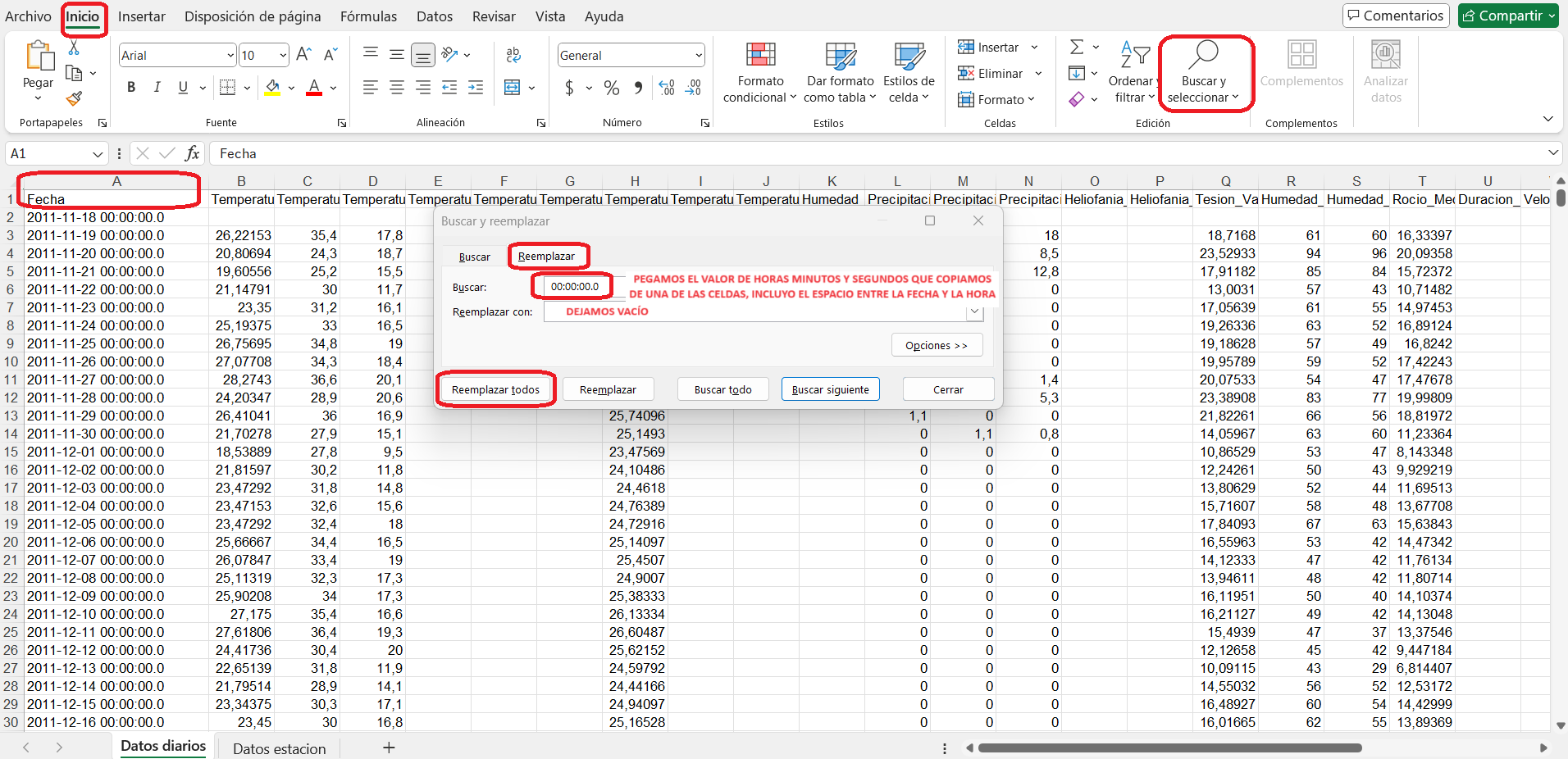
Campo Fecha (A) transformado.

Luego de transformar todas las columnas se vuelve a guardar el archivo.
Ahora se puede trabajar con él.
Declaración de tablas
Insertar > Tabla
En el ámbito del procesamiento de datos, especialmente cuando se trabaja con grandes volúmenes de información, es fundamental utilizar herramientas y técnicas que faciliten la gestión, el análisis y la visualización eficiente de los datos. Microsoft Excel, una de las aplicaciones más utilizadas para el manejo de datos, ofrece la funcionalidad de convertir rangos de datos en tablas estructuradas. Esta característica, aunque a menudo subestimada, proporciona numerosas ventajas que mejoran significativamente la eficiencia y precisión del trabajo con datos extensos.
A continuación, se presentan las ventajas de usar tablas en Excel y su utilidad específica en el procesamiento de grandes volúmenes de datos.
Organización y claridad
Nombres y etiquetas. Las tablas permiten asignar nombres y etiquetas a las columnas, lo que facilita la comprensión y organización de los datos.
Formato automático. Excel aplica automáticamente un formato consistente a las tablas, lo que mejora la legibilidad.
Facilidad de manejo de dato
Ordenar y filtrar. Las tablas vienen con controles automáticos para ordenar y filtrar los datos, lo que facilita encontrar y analizar información específica rápidamente.
Referencias estructuradas. Permiten el uso de referencias estructuradas, es decir, referirse a columnas por sus nombres en lugar de por sus coordenadas, lo que hace que las fórmulas sean más comprensibles y menos propensas a errores.
Automatización y actualización dinámica
Expansión automática. Al agregar nuevos datos a una tabla, Excel automáticamente expande la tabla para incluir los nuevos datos, sin necesidad de ajustar manualmente los rangos de datos.
Fórmulas y cálculos automáticos. Las fórmulas aplicadas en una columna de una tabla se copian automáticamente a nuevas filas, lo que ahorra tiempo y reduce errores.
Herramientas de análisis y resumen
Tablas dinámicas. Las tablas en Excel son compatibles con otras tablas dinámicas, lo que permite resumir y analizar grandes volúmenes de datos de manera eficiente.
Gráficos dinámicos. Facilitan la creación de gráficos dinámicos que se actualizan automáticamente al modificar los datos en la tabla.
Protección de datos y mantenimiento
Conformidad de datos. Las tablas ayudan a mantener la conformidad y consistencia de los datos, ya que es más fácil detectar y corregir errores en un formato estructurado.
Fórmulas estables. Las referencias estructuradas dentro de las tablas se ajustan automáticamente cuando se insertan o eliminan filas y columnas, lo que mantiene la integridad de las fórmulas.
Eficiencia en la gestión de datos
Manejo de datos masivos. Las tablas permiten manejar grandes conjuntos de datos de manera más eficiente, lo que proporciona herramientas para filtrar, ordenar y agrupar datos sin afectar el rendimiento.
Optimización del rendimiento. Excel optimiza internamente el uso de tablas, lo que mejora el rendimiento en comparación con el manejo de rangos no estructurados.
Automatización y reducción de errores
Actualización automática: La expansión automática y la replicación de fórmulas reducen la necesidad de ajustes manuales, lo que disminuye el riesgo de errores humanos.
Referencias consistentes. Las referencias estructuradas son menos propensas a errores, lo que es crucial cuando se trabaja con grandes volúmenes de datos donde los errores pueden ser difíciles de detectar.
Mejor análisis y visualización
Análisis avanzado. La compatibilidad con tablas dinámicas y gráficos facilita el análisis avanzado de datos, lo que permite resumir y visualizar información compleja de manera efectiva.
Dashboards y reportes. Facilitan la creación de dashboards interactivos y reportes, esencial para la toma de decisiones basada en datos.
Ejemplo práctico. Si se dispone de una gran cantidad de datos sobre rendimientos de cultivos en diferentes regiones y años, al convertir estos datos en una tabla de Excel se podría:
- ordenar y filtrar fácilmente por año, región o tipo de cultivo;
- crear rápidamente una tabla dinámica para resumir los rendimientos promedio por región y año.
Fórmulas consistentes. Aplicar fórmulas para calcular totales o promedios simplificaría, ya que las fórmulas se aplican automáticamente a nuevas filas.
Cabe destacar que declarar tablas en Excel es una práctica poderosa y eficiente que mejora la gestión, el análisis y la visualización de grandes volúmenes de datos, a la vez que proporciona herramientas y funcionalidades que optimizan tanto el rendimiento como la precisión en el procesamiento de datos. Utilizar tablas estructuradas en Excel no solo facilita el manejo de datos masivos, sino que también reduce errores, mejora la claridad y organiza la información de manera más eficiente, lo cual es crucial en cualquier ámbito que requiera un análisis de datos riguroso y detallado.
Paso a paso con tablas
Primero: insertar la Tabla (declarar tabla).
Para ello posicionarse en la celda A1 y luego tocar la tecla Ctrl y la tecla T (Ctrl + T), esto es un atajo para insertar una tabla.
También es posible seleccionar todo, ir a Insertar en el Menú > Tabla.
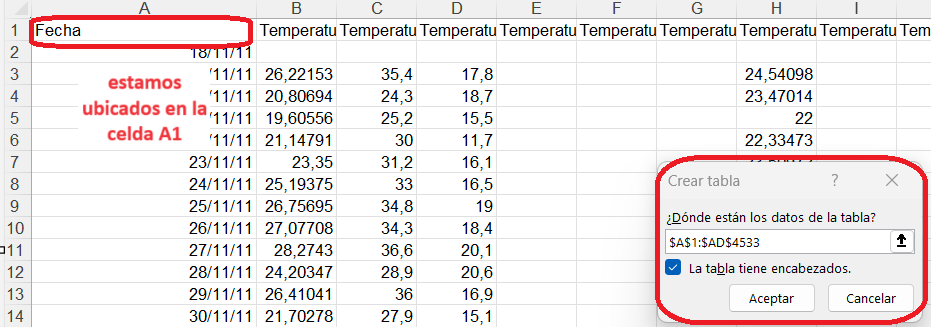
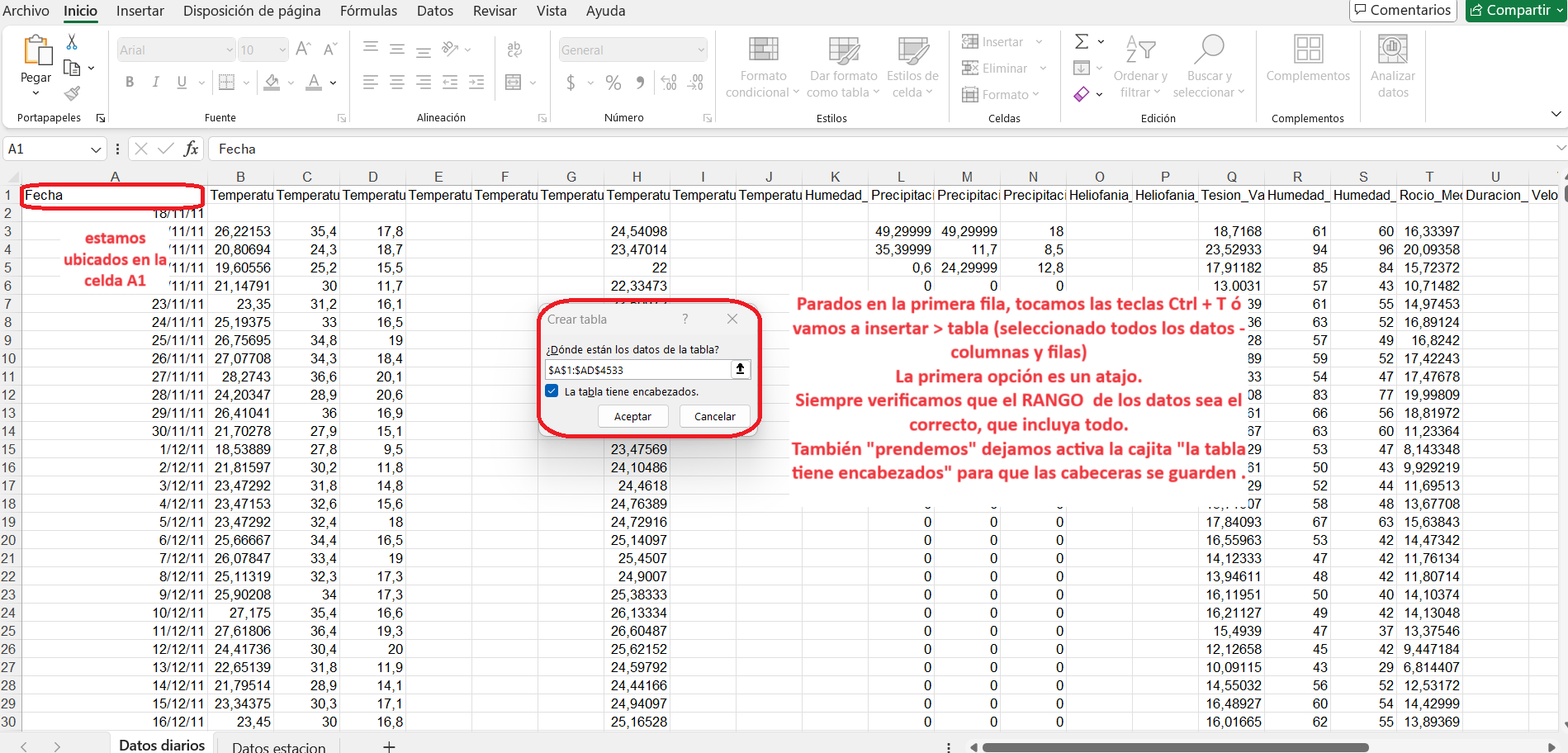
Luego, se visualizará el archivo transformado, con el rango que se ha convertido en Tabla y posee estilo propio, y las propiedades y posibilidades de análisis descriptas con anterioridad.
Ejemplo:
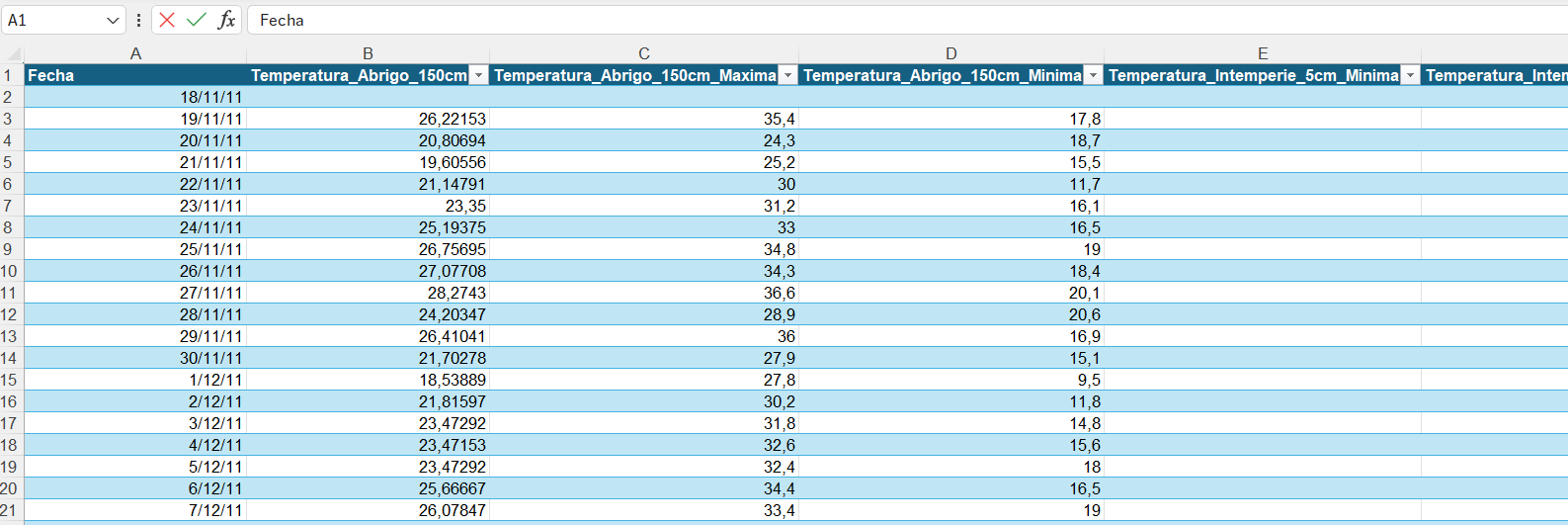
¿Qué es una tabla dinámica?
Una tabla dinámica (PivotTable) es una herramienta interactiva de Excel que permite resumir, analizar, explorar y presentar grandes volúmenes de datos de una manera sencilla y flexible. Las tablas dinámicas facilitan reorganizar los datos para ver diferentes resúmenes y detalles, sin necesidad de alterar el conjunto de datos original.
Para qué sirve una tabla dinámica
Resumen de datos. Permite realizar agregaciones como sumas, promedios, conteos y otras operaciones matemáticas sobre los datos, lo que proporciona resúmenes rápidos y concisos.
Análisis de datos. Facilita el filtrado, el ordenamiento y la agrupación de datos, lo que permite analizar diferentes aspectos de los datos de forma dinámica.
Visualización de datos. Ayuda a crear gráficos dinámicos que se actualizan automáticamente al modificar la tabla dinámica; esto proporciona una representación visual clara de los datos.
Toma de decisiones. Ayuda a identificar tendencias y patrones en los datos, cruciales para la toma de decisiones informadas en el sector agrario.
Utilidad en el análisis profesional
Para técnicas agrarias y técnicos agrarios, las tablas dinámicas son útiles en el análisis de datos agrometeorológicos. Permiten, entre otras, las acciones que se describen a continuación:
Monitoreo y control. Analizar los datos meteorológicos diarios para monitorear las condiciones climáticas y tomar decisiones sobre riego, siembra y cosecha.
Identificación de tendencias. Evaluar tendencias a lo largo del tiempo, como variaciones estacionales en la temperatura y las precipitaciones, lo cual es esencial para planificar las actividades agrícolas.
Optimización de recursos. Analizar datos históricos para optimizar el uso de recursos como agua y fertilizantes, basándose en patrones climáticos.
Cómo crear y usar una tabla dinámica en el análisis
Paso 1. Selección de datos
Primero, seleccionar los datos a analizar. En este caso, se utiliza la hoja "datos diarios" del archivo.
Paso 2. Inserción de la tabla dinámica
Seleccionar el rango de datos. Seleccionar el rango completo de datos de la hoja "datos diarios".
Insertar tabla dinámica. Ir a la pestaña "Insertar" en el menú de Excel y seleccionar "Tabla Dinámica".
Configurar la Tabla Dinámica. En el panel de campos de tabla dinámica, arrastrar los campos a las áreas de Filtro, Columnas, Filas y Valores según cómo se desea resumir los datos.
Paso 3. Configuración y análisis
Agrupación por fecha. Agrupar los datos por meses o años para analizar las tendencias temporales.
Suma y promedio de variables. Calcular la suma de precipitación total y el promedio de temperaturas para diferentes períodos y estaciones.
Filtros y segmentaciones. Usar filtros para analizar datos específicos, como periodos de sequía o temperaturas extremas.
Ejemplo Práctico
Iniciar el análisis de los datos de la Tabla declarada, con los miles de datos descargados de la unidad meteorológica en línea.
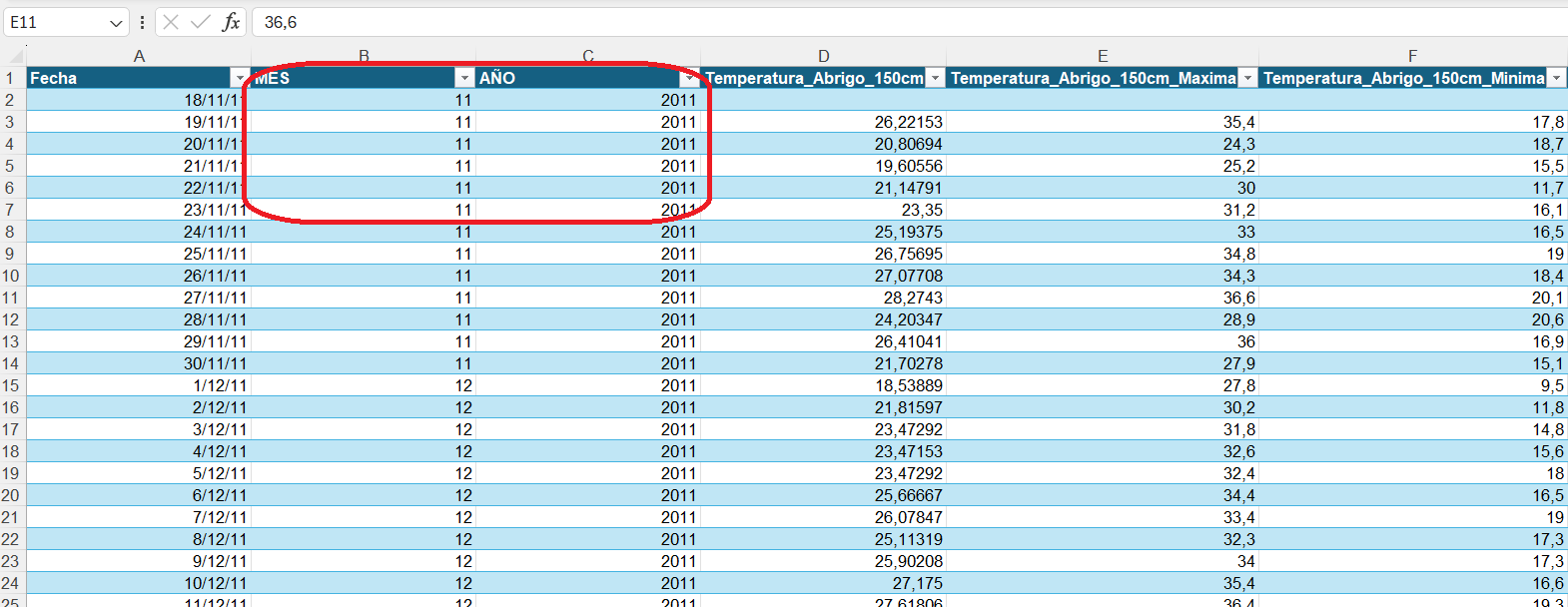
Primero, insertar dos nuevas columnas, mes y año.
Para ello, a la derecha de la primera columna (fecha) insertar dos nuevas columnas. La primera columna se denominará MES. La segunda, AÑO.
En MES se utilizará la fórmula =MES (leer la información de la primera fecha para calcular el mes).
En Año se utilizará la fórmula =AÑO (leer la información de la primera fecha para calcular el año).
Como los valores obtenidos tendrán el formato de una fecha ya que heredaron el formato numérico de la columna fecha, se cambiará el formato de los números (la manera en la que se visualiza el número en las columnas). Para cambiar el formato de fecha a número, se selecciona primero la columna MES y luego la columna AÑO.
Hacer clic con el botón derecho del mouse en > formato de celdas > número> número (SIN decimales)
Los datos se visualizarán así:
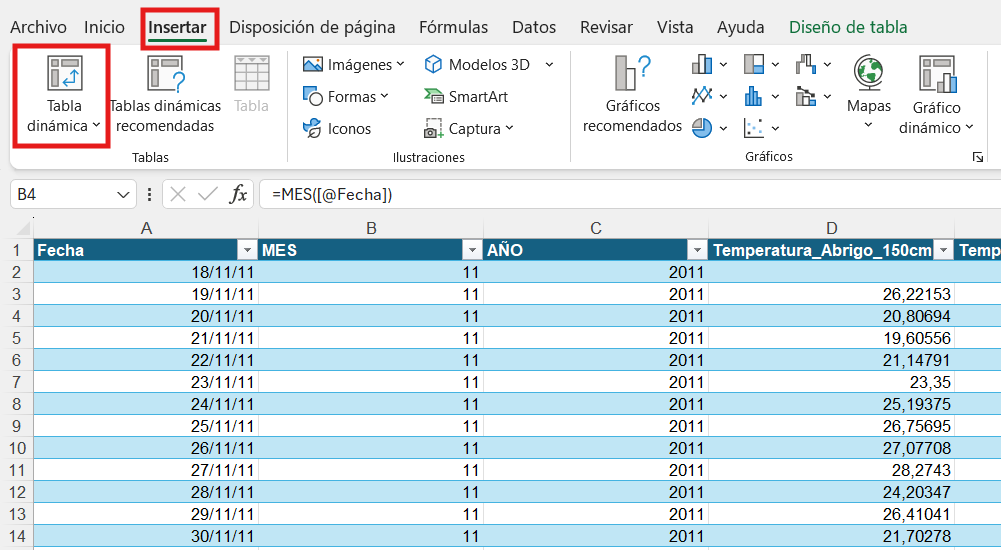
Insertar una tabla dinámica (desde cualquier celda de la Tabla declarada en el punto anterior) desde el menú principal.
Insertar > Tabla dinámica.
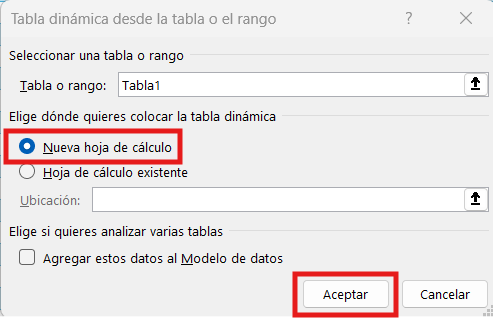
Ubicar la tabla dinámica en hoja nueva.
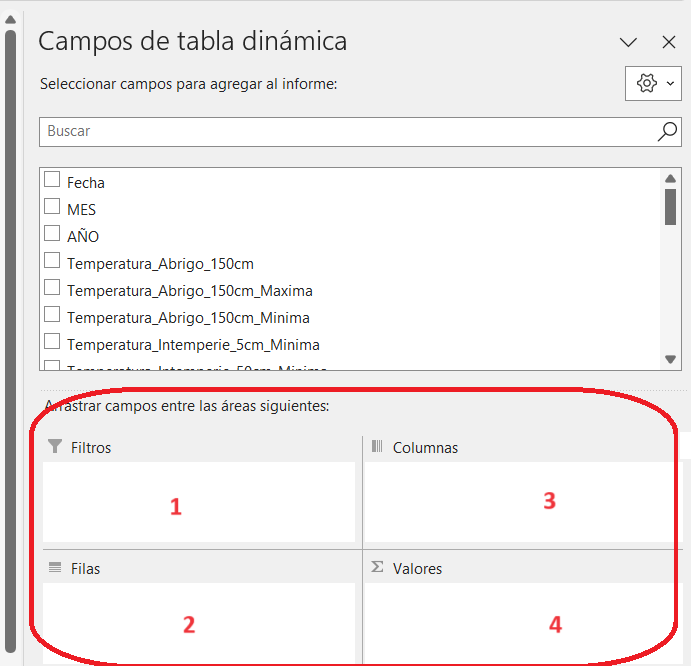
Una tabla dinámica es un cuadro de doble entrada con cuatro cuadrantes para su construcción.
En 1, se pueden ubicar filtros, cabeceras de campos que permiten “filtrar” criterios de análisis.
En 2, se colocan cabeceras de campos de la tabla (los títulos de las columnas) que hagan referencia a criterios que permitan organizar la información; en este caso, por ejemplo, fechas, meses, años.
En 3, también se pueden colocar este tipo de cabeceras, siempre de referencia, para referenciar con mejor criterio en el análisis de datos. Se puede también omitir colocar campos aquí.
En 4, se colocan los campos (títulos de cabeceras de columnas) que requieren cálculos, por ejemplo sumar, promediar, contar, calcular desvíos, realizar operaciones entre otras posibilidades. Es tal vez el corazón de la tabla dinámica, donde se colocan las columnas que interesa comprender: cómo se distribuyen los datos y qué se puede calcular de ellos para comprenderlos.
Cuando se tienen miles de datos, para comprenderlos es necesario hacer cálculos. Esto requiere, la mayoría de las veces, de la realización de tablas dinámicas.
Arrastrando los nombres de las cabeceras a los cuadrantes predeterminados, se arma la tabla.
Ejemplo para analizar el promedio de temperaturas mensuales (T° de abrigo) de cada mes.
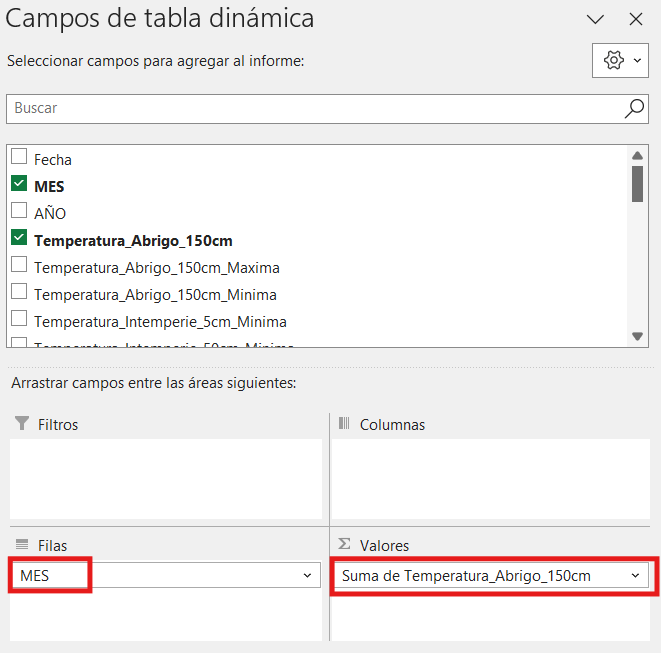
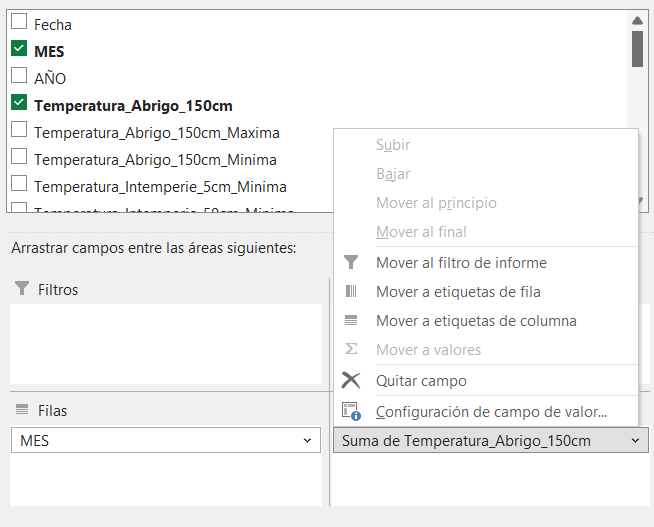
Primero se necesita la T° promedio de cada mes, la tabla dinámica por defecto suma los valores de cada día de cada mes medido. Por lo tanto, hay que cambiar ahora la operación aritmética. Se cambia SUMA por PROMEDIO. Hacer clic en el desplegable a la derecha del nombre del campo y elegir CONFIGURACIÓN DE CAMPO DE VALOR > PROMEDIO. Luego el cálculo será el correcto.
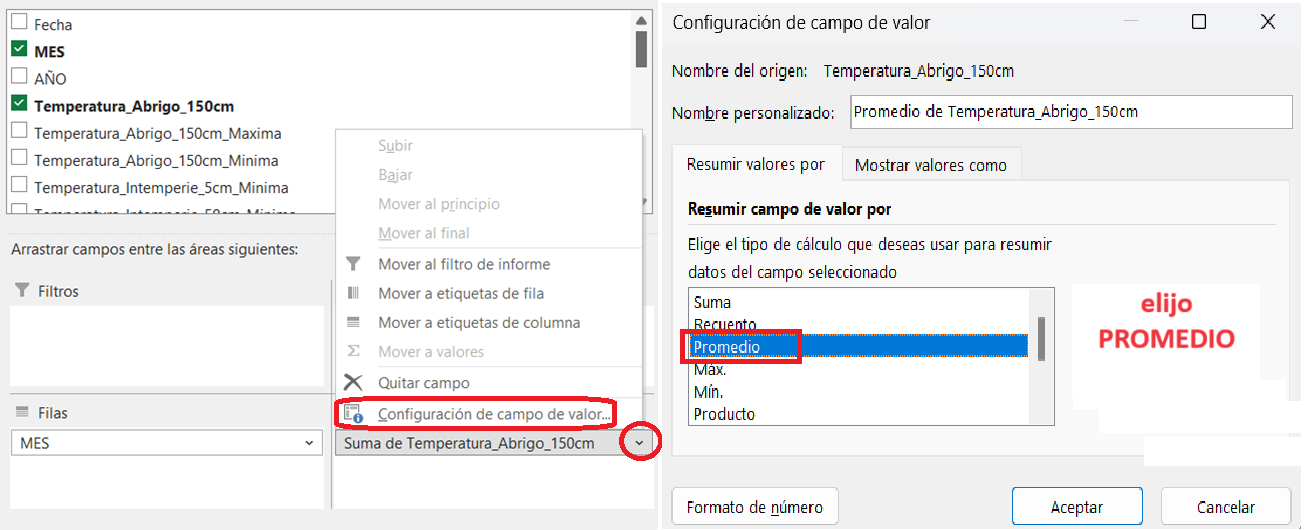
Ahora se visualizarán los datos ordenados por mes y promediados, es decir el promedio de T° media de cada mes de una serie temporal desde 2011.
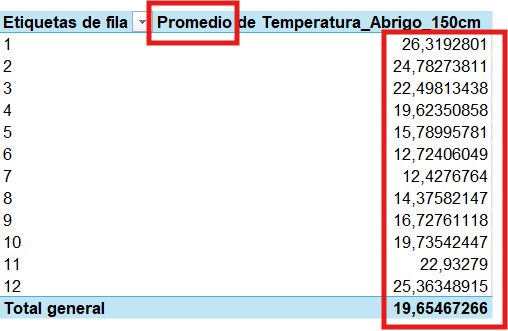
Al hacer clic en cualquier lugar de la tabla dinámica, sólo se debe insertar un gráfico que ya está listo y asociado a estos datos.
Luego, posicionarse en una celda de la tabla dinámica > insertar > gráfico de barras verticales.
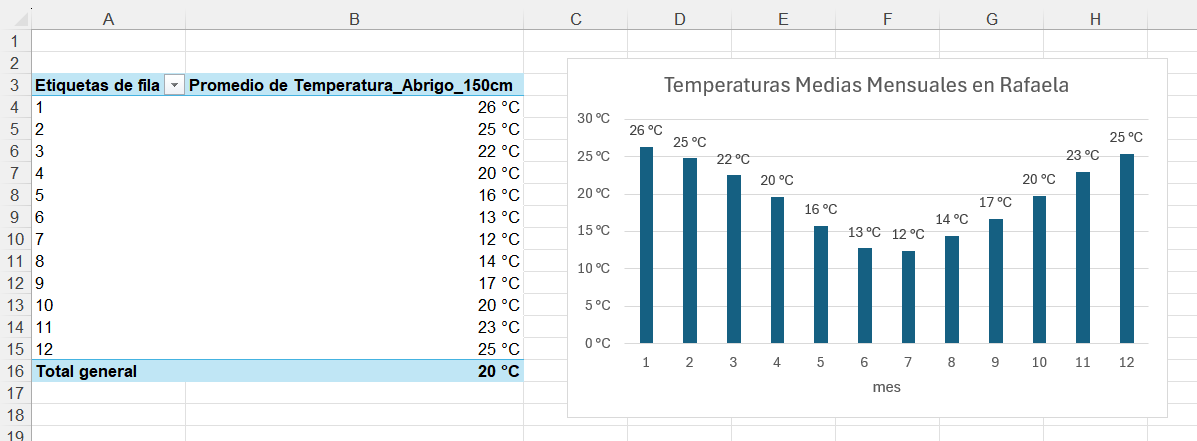
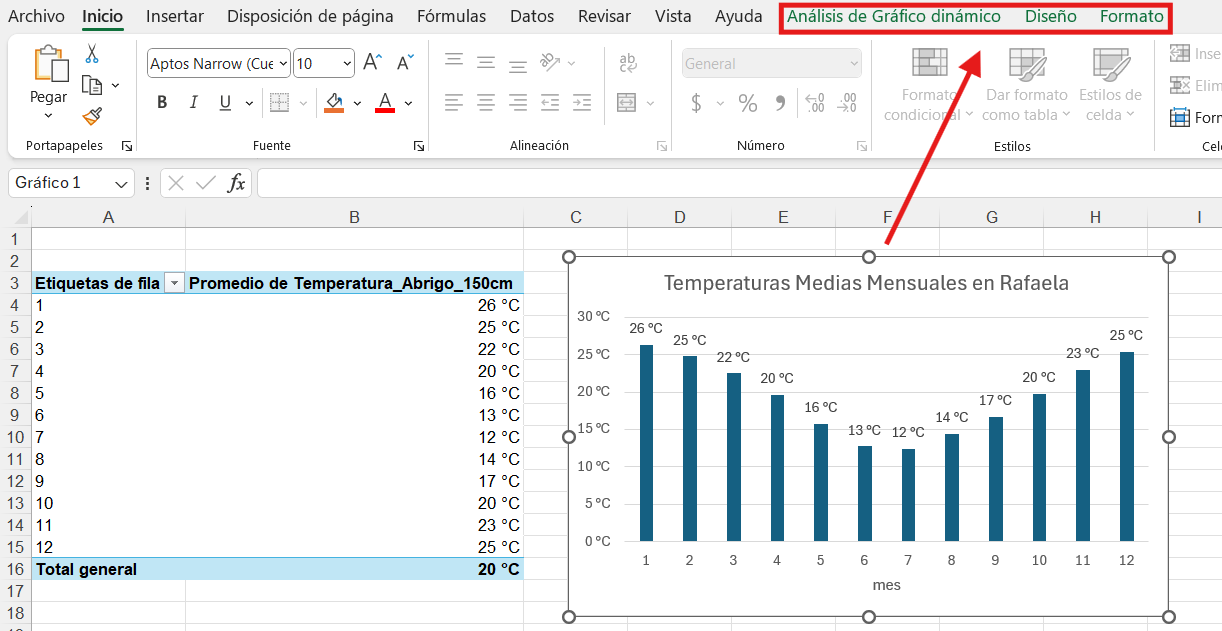
Si se tiene seleccionado el gráfico creado en la parte superior del menú, a la derecha se visualizará el menú contextual de gráficos que me permite editarlo.
Séptimo momento. Actividad final
Mediante esta propuesta, las y los estudiantes explorarán el procesamiento y análisis de datos agrometeorológicos, utilizando Excel, con el objetivo de comprender mejor las condiciones climáticas que afectan a la producción agrícola en su región. A través del uso de tablas dinámicas, aprenderán a resumir y visualizar grandes volúmenes de datos, lo que facilitará la toma de decisiones informadas en el ámbito agrario.
Objetivos de enseñanza
- Desarrollar habilidades en el manejo de datos. Enseñar a las y los estudiantes a descargar, procesar y analizar datos agrometeorológicos utilizando herramientas avanzadas de Excel.
- Fomentar el trabajo en equipo. Promover la colaboración y el trabajo en equipo en la elaboración de informes técnicos y presentaciones orales.
- Aplicar conocimientos estadísticos. Aplicar conceptos estadísticos –como media, mediana, moda y desviación estándar– en el análisis de datos agrometeorológicos.
- Interpretar y comunicar resultados. Desarrollar habilidades para interpretar los resultados del análisis y comunicar las conclusiones de manera efectiva.
Actividades
- Seleccionar una unidad meteorológica en línea cercana a la escuela agraria
- Las y los estudiantes deben identificar y seleccionar una estación meteorológica en línea cercana a su ubicación. Utilizarán las unidades meteorológicas del Sistema de Información y Gestión Agrometeorológica de INTA
- Descargar y procesar los datos siguiendo los pasos aprendidos
- Utilizar las herramientas proporcionadas para descargar datos históricos de la unidad meteorológica seleccionada.
- Procesar estos datos en Excel, convirtiéndolos en una tabla estructurada y creando tablas dinámicas para el análisis.
- Elaborar un informe técnico que describa el perfil agrometeorológico de la región seleccionada
- En grupos, las y los estudiantes deben analizar diferentes variables agrometeorológicas como el promedio de temperatura, las precipitaciones, las temperaturas máximas y mínimas, y la humedad relativa.
- El informe debe incluir no solo los valores centrales (media, mediana, moda), sino también las dispersiones de las mismas (desviación estándar), y dará cuenta de cómo estas variaciones afectan el análisis.
- Presentar los resultados en una instancia de exposición oral
- Cada grupo debe preparar una presentación oral en la que se expliquen los métodos utilizados y las conclusiones obtenidas del análisis.
- La presentación debe incluir comparaciones entre la región local y otras zonas de Argentina, y destacar las diferencias y similitudes en las variables analizadas.
Consigna detallada
- Seleccionar la unidad meteorológica
- Buscar en el sitio web del INTA o en otros recursos disponibles una estación meteorológica en línea cercana.
- Descargar los datos meteorológicos disponibles para el período de estudio (por ejemplo, los últimos 5 años).
- Procesar los datos en Excel
- Importar los datos descargados a Excel y convertirlos en una tabla estructurada.
- Utilizar tablas dinámicas para analizar las variables seleccionadas: promedio de temperatura, precipitaciones, temperaturas máximas y mínimas mensuales, humedad relativa, entre otras.
- Calcular y analizar los valores centrales (media, mediana, moda) y las dispersiones (desviación estándar) de cada variable.
- Elaborar el informe técnico
- El informe debe incluir una introducción, metodología, resultados y conclusiones.
- Describir el perfil agrometeorológico de la región, destacar las principales tendencias y variaciones observadas.
- Comparar estos resultados con los de otras zonas de Argentina, y explicar las diferencias y sus posibles implicaciones agronómicas.
- Preparar y realizar la presentación oral
- Preparar una presentación de 10-15 minutos en la que se expongan los resultados del análisis.
- Cada integrante del grupo debe participar en la presentación, explicando una parte del análisis y sus conclusiones.
- Responder preguntas del resto de la clase, demostrando una comprensión profunda de los datos y del análisis realizado.
Conclusión
Esta actividad permitirá a las y los estudiantes aplicar conocimientos teóricos en un contexto práctico, y desarrollar habilidades analíticas y de presentación esenciales para su futuro profesional. Al final de la actividad, se espera que puedan manejar y analizar datos agrometeorológicos, así como mejorar su capacidad para trabajar en equipo y comunicar sus hallazgos de manera clara y efectiva.
1 Prueba t: es un método estadístico que se utiliza para determinar si hay una diferencia significativa entre las medias de dos grupos. Se emplea comúnmente en estudios donde se comparan las medias de dos muestras independientes o relacionadas para evaluar si las diferencias observadas son probablemente debidas al azar o si reflejan diferencias reales en la población.
ANOVA (Análisis de Varianza): es una técnica estadística utilizada para comparar las medias de tres o más grupos para determinar si al menos una de las medias es significativamente diferente de las demás. ANOVA analiza la variabilidad dentro de cada grupo y entre los grupos para evaluar si las diferencias observadas son significativas.