Momentos de esta propuesta:

1. 1 Retomar Primer Ciclo.
2. 2Circunferencia y Círculo.
3. 3 Ángulos y Triángulos.
4. 4Cuadriláteros.

Acerca de la organización del material para estudiantes

El material “Parte 4: Cuadriláteros”¹ está separado por grandes títulos, que llamaremos apartados, éstos contienen grupos de problemas que permiten aproximarse a cierta porción del conocimiento geométrico en torno a estas figuras. Cada título hace referencia a los temas que estudiarán las y los estudiantes, por ejemplo “Estudiar algunos cuadriláteros” o “Estudiar algunas características de los paralelogramos”. Los problemas de cada apartado se proponen para resolver individualmente o, a decisión de cada docente, en parejas. Luego de las resoluciones será interesante coordinar momentos de intercambio colectivo en los que sea posible difundir y analizar estrategias, soluciones, errores y/o conclusiones; más adelante nos explayaremos sobre estos aspectos. En ciertos apartados se ha agregado un subtítulo en letra itálica que informa cuáles son los instrumentos geométricos que será necesario tener disponibles para resolver los problemas allí incluidos, con la intención de que tanto docentes como estudiantes puedan anticiparlo.

Al igual que venimos proponiendo en otros materiales, incluimos instancias de reflexión sobre lo realizado. Estas situaciones plantean un retorno sobre los problemas matemáticos y sobre los diversos procedimientos desplegados para resolverlos, entendiendo que detenerse y volver atrás es fundamental para avanzar; los conocimientos movilizados durante la resolución suelen funcionar de manera implícita y podrían permanecer en ese estado de no mediar situaciones que requieran su explicitación. Nos referimos a las instancias “Para revisar y seguir pensando”, en las que se propone la reflexión, el análisis y/o el registro de lo realizado a propósito de un conjunto o subconjunto de problemas de un mismo apartado. Estos nuevos acercamientos a los problemas ya resueltos se proponen, también, con diferentes modalidades de organización (individual, en pequeños grupos o en grupo total) mediados por la o el docente y usando el pizarrón como soporte para el registro. Además, en estas secciones se pretende poner en juego, en nuevos problemas, lo trabajado y aprendido en el apartado correspondiente. Presentamos a continuación ejemplos de estas instancias:

Para revisar y seguir pensando (pág. 4)

Para revisar y seguir pensando (pág. 16)

La escritura de conclusiones está planteada en forma colectiva, sin embargo, en otros momentos podría ser propuesta en parejas o pequeños grupos. Las situaciones en las que estudiantes le dictan a la o el docente las conclusiones para que queden en un cartel o en el pizarrón son buenas oportunidades para revisar las ideas iniciales, para profundizar en el análisis de las argumentaciones o para analizar errores. Es importante que esos registros resulten claros para todas y todos y que puedan reconocer allí aquello que circuló en la clase y puede ser reutilizado. Esas escrituras podrán ser retomadas y revisadas a medida que se transforman los conocimientos de las y los estudiantes; por lo que será necesario que estén a la vista del grupo, por ejemplo, en grandes carteles en el aula o pequeños registros en carpetas o cuadernos.

Incluimos, asimismo, algunos recuadros con texto y dibujos que podrían actuar de ayuda-memoria, toma de notas u orientaciones para el trabajo, bajo los títulos de “Para recordar” y “Para tener en cuenta”. Los primeros se proponen con doble intención, por un lado, recordar algunas características o propiedades ya conocidas de las figuras geométricas y, por otro lado, anticipar algo nuevo que será necesario recordar. Los segundos apuntan a tomar nota de cómo usar ciertos instrumentos para la construcción o trazado de objetos geométricos, por ejemplo, regla no graduada, escuadra, transportador. También se incluyen en estos recuadros notas para recordar alguna de las propiedades o características trabajadas. Todos se incluyen con la intención de que estén “a mano” durante la resolución de nuevos problemas.

Podría ser interesante que las y los estudiantes vayan construyendo una sección dentro de la carpeta que compile, para su consulta, la información valiosa ofrecida en estos recuadros como así también los registros personales y colectivos que van elaborando a medida que avanzan en la sistematización de los conocimientos que circulan en las clases.

A continuación, se presentan ejemplos de estos recuadros:

Para recordar (pág. 6)

Para tener en cuenta (pág. 4)²

La variedad de modalidades de organización también representa un recurso potente para dar lugar a las diversas voces y conocimientos de las chicas y los chicos. En ocasiones, es importante reservar un primer acercamiento individual para que cada estudiante tenga un espacio propio para analizar el problema geométrico propuesto, movilizar los conocimientos que considere pertinentes y ensayar un primer camino de resolución. En otras, el trabajo individual se plantea al final de un conjunto de clases en parejas o grupos, dada la potencialidad de las interacciones entre pares para la construcción y el avance de los conocimientos, con la intención de favorecer una mayor autonomía para usar lo que se aprendió luego de un tiempo de estudio colectivo. 

Sobre el uso de los instrumentos geométricos

Incluimos en algunos apartados y/o problemas el uso de algunos de los instrumentos que las y los estudiantes deben aprender a utilizar para copiar o construir objetos geométricos. Es importante señalar, como ya se dijo en páginas anteriores, que uno de los cambios que presenta la actividad geométrica durante el Segundo Ciclo con respecto al Primer Ciclo refiere a los modos de validación y argumentación, es decir, de qué manera las y los estudiantes darán cuenta de la validez de las respuestas y procedimientos que han utilizado en la resolución de las situaciones dadas. Por tal motivo es central en el Segundo Ciclo analizar el papel que juega la medición dentro de los problemas geométricos. Ésta siempre implica la presencia de errores, es decir, las mediciones pueden ser más o menos precisas, pero nunca exactas; por tal razón, cualquier argumento basado en mediciones tendrá un componente de aproximación. En cambio, es necesario pasar progresivamente a argumentos basados en propiedades o características de la figura en cuestión y no del dibujo particular realizado. Por ejemplo, si el problema está centrado en la búsqueda de la amplitud de un ángulo, la medición con el transportador arrojará respuestas como “mide 61º”, o “mide 59º”, o “mide 60º”; será necesario discutir con la clase cuáles de esas mediciones son aproximadas. 

El trabajo con compás, transportador, regla graduada, regla no graduada y escuadra es un valioso recurso para propiciar el estudio de ciertas propiedades de las figuras. Es necesario, por lo tanto, enseñar a utilizarlos sin perder de vista su propósito. En el material para estudiantes, en el apartado que aborda el trazado de rectas y segmentos paralelos y perpendiculares, se presentan problemas “para enseñar a usar la escuadra” con la intención de ayudar a construir dichas ideas.

Otro aspecto importante a tener en cuenta en el trabajo geométrico es el tipo de hoja que se propone usar para la resolución de los problemas, pues según sea cuadriculada o lisa se promueve o no la puesta en primer plano de algunas propiedades o características de las figuras que se pretenden estudiar. Por ejemplo, si se solicita la construcción de un rectángulo en hoja lisa, los estudiantes deberán buscar el modo de garantizar la perpendicularidad de lados consecutivos, cuestión que no se constituye como centro del problema si la hoja es cuadriculada. Es por esta razón que algunos de los problemas de construcción y copiado podrán proponerse inicialmente en hoja cuadriculada, y luego en hoja lisa, de modo de poner en juego las características que se quieren estudiar.³

Sobre el contenido y la organización del documento

La propuesta que presentamos en esta oportunidad aborda la enseñanza de las figuras geométricas. Detallamos a continuación los contenidos incluidos:

• Construir y analizar construcciones de cuadrados, rectángulos, rombos y paralelogramos como medio para explorar algunas de sus propiedades referidas a igualdad y paralelismo de lados, igualdad de ángulos, suma de ángulos interiores, igualdad y perpendicularidad de las diagonales, etc. Análisis de la cantidad de soluciones posibles. Analizar posibles clasificaciones de cuadriláteros (sin necesidad de memorizarlas).
• Iniciación en la resolución de problemas deductivos que implican determinar el valor de un lado o de un ángulo a partir de los datos que se ofrecen y de las propiedades de triángulos y cuadriláteros.

En la misma línea que venimos planteando en los materiales producidos por la Dirección Provincial de Educación Primaria entre 2020 y 2022 (entre los que se encuentran las propuestas de intensificación de la enseñanza), los problemas que se incluyen proponen una progresión y una secuenciación que apuntan a movilizar ciertos conocimientos con la intención de generar nuevos aprendizajes. Es importante tener en cuenta, entonces, que las y los estudiantes ingresan a estos contenidos a partir de lo que saben acerca de las figuras geométricas y que han construido tanto dentro de la escuela como fuera de ella. Es posible entonces anticipar que los procedimientos iniciales de copiado y construcción de figuras que las niñas y los niños desplieguen tendrán un fuerte anclaje en los conocimientos que han elaborado al resolver otros problemas similares. Cada docente podrá reconocer que para algunas y/o algunos estudiantes no será necesario detenerse por mucho tiempo en esas propuestas menos complejas dado que las resuelven sin dificultad. Sin embargo, es posible que para otras y otros sea preciso destinar un poco más de tiempo a estudiar aquello con lo que no han tenido oportunidades suficientes de interactuar en años anteriores.

En el material para estudiantes se encuentran los siguientes apartados:

• En los apartados Estudiar algunos cuadriláteros, Rectas y segmentos paralelos y perpendiculares, Estudiar algunas características de los paralelogramos se apunta al trabajo relacionado con construir y analizar construcciones de cuadrados, rectángulos, rombos y paralelogramos como medio para explorar algunas de sus propiedades referidas a igualdad y paralelismo de lados e igualdad de ángulos.
• En los apartados Problemas para estudiar las diagonales de los cuadrados y de los rectángulos, Problemas para estudiar las diagonales de los rombos y de los paralelogramos, Cuadriláteros a partir de lados y diagonales el trabajo gira en torno a resolver problemas que demandan la suma de ángulos interiores de los cuadriláteros, igualdad y perpendicularidad de las diagonales, etc., así como a analizar la cantidad de soluciones y posibles clasificaciones de cuadriláteros (sin necesidad de memorizarlas).
• En el último apartado, Problemas para explorar los ángulos de los cuadriláteros, se propone integrar el trabajo realizado sobre las construcciones de cuadriláteros a partir de las medidas de los ángulos e iniciar a los estudiantes en la resolución de algunos problemas deductivos (tales como aquellos que implican determinar el valor de un lado o ángulo considerando los datos que se ofrecen y apelando a las propiedades de triángulos y cuadriláteros).

El conjunto de problemas que propone cada apartado contribuye a la construcción y problematización del siguiente. Es así que las situaciones iniciales que se presentan en cada caso se apoyan en el uso de los conocimientos que las y los estudiantes puedan tener disponibles a partir de lo movilizado anteriormente.

A continuación, presentaremos algunas orientaciones didácticas para cada apartado.

Orientaciones didácticas

Para comenzar el trabajo sobre cuadriláteros en este material se propone el apartado Estudiar algunos cuadriláteros (pág. 2). Allí se han incluido situaciones en las que es necesario copiar y completar figuras en hoja lisa apelando al uso de los instrumentos geométricos que se mencionan. Se espera que las chicas y los chicos pongan en juego algunos conocimientos sobre estas figuras geométricas construidos anteriormente, dentro o fuera de la escuela.

El problema 1 (pág. 2-3) plantea realizar copias en hoja lisa y solo se habilita el uso de regla no graduada, compás y escuadra. La intención de excluir el uso de la regla graduada es promover que se traslade la medida de segmentos con el compás y sin cuantificar su longitud. La escuadra se habilita para construir ángulos rectos y la regla no graduada -que puede ser reemplazada por la parte no graduada de la escuadra- para trazar segmentos sin cuantificar sus medidas. 

En este problema puede notarse la progresión en la complejidad de las copias a realizar, por ejemplo, el ítem b- incluye un cuadrado dentro de un rectángulo. Los lados de ambas figuras no tienen puntos de contacto, lo cual representa una dificultad dado que será necesario considerar la distancia entre cada vértice del cuadrado interior y los lados del rectángulo exterior. Finalmente, la última figura dada no está sobre hoja cuadriculada y su posición no es la más habitual (lados paralelos a los bordes de las hojas). Será necesario usar la escuadra para asegurarse que los ángulos de dicha figura sean rectos, es decir que se trate efectivamente de un cuadrado. Resultará interesante conversar con las y los estudiantes acerca de la posición en que dibujan las copias, si respetan o no la de la figura original. Asimismo, se podrá conversar sobre algún modo de validar las copias, es decir de determinar si coinciden con la figura dada. Si para ello algunas y algunos estudiantes proponen superponer ambas imágenes, las maestras y los maestros podrán dirigir la discusión hacia el uso de argumentos basados en las características de las figuras. Por ejemplo, frente al último ítem: “los cuatro ángulos son rectos como en la figura porque usamos la escuadra y los cuatro lados miden lo mismo que la original porque usamos el compás para asegurarnos eso, por último, la diagonal va de un vértice a otro. Así está bien hecho”. 

En los problemas 2 y 3 (pág. 3-4) se busca completar el dibujo con la intención de recuperar los conocimientos sobre triángulos y colaborar en la explicitación de relaciones entre triángulos y cuadriláteros, considerando algunas características de los cuadriláteros involucrados. Resaltar este vínculo es interesante porque permite utilizar los conocimientos disponibles sobre una figura conocida al estudiar una “nueva”. Así, en el problema 2 deberán utilizar que los cuadrados tienen sus cuatro lados iguales y que el triángulo dado ofrece dos de sus lados iguales. A su vez, podrán apoyarse en que se trata de un triángulo rectángulo, cuyo ángulo recto será uno de los ángulos del cuadrado. Es posible que algunas chicas y algunos chicos no tomen en cuenta esta característica y que, sin embargo, la construcción les quede correcta porque dibujan otro triángulo de modo que los cuatro lados midan lo mismo que los catetos del triángulo dado. Será necesario conversar con ellas y ellos, luego de resolver estos dos problemas (el 2 y el 3), acerca de qué se tuvo en cuenta para la construcción. Esta es la intención del espacio de trabajo en parejas propuesto en el recuadro denominado Para revisar y seguir pensando (pág. 4). De manera implícita, las y los estudiantes pondrán en juego que cada diagonal divide a los cuadrados y a los rectángulos en dos triángulos rectángulos iguales. Esta característica será estudiada a propósito de las diagonales en apartados posteriores.

Si bien las situaciones del apartado Rectas y segmentos paralelos y perpendiculares (pág. 4) no giran en torno al tratamiento de cuadriláteros de manera explícita, involucran conocimientos que permiten aprender otras características de estas figuras. Por ejemplo, para la construcción de cuadrados será necesario el trazado de lados paralelos y perpendiculares y para la construcción de paralelogramos será necesario tener en cuenta segmentos oblicuos y paralelos. En el subtítulo del apartado se indica que solo puede usarse escuadra y regla graduada, pues con estos dos instrumentos es posible trazar segmentos paralelos y perpendiculares a otros dados. El recuadro Para tener en cuenta (pág. 6) ofrece una explicación sobre cómo se utilizan estos instrumentos para tal fin. 

Es posible que sea necesario tomarse unos minutos para ayudar a comprender este recuadro, explicitando el movimiento necesario de la escuadra y el sostenimiento firme de la regla para el trazado de paralelas.

En los primeros dos problemas de este apartado (pág. 2-3) no se mencionan las palabras “perpendicular” ni “paralelo” pues estas relaciones aparecen de manera exploratoria. Más adelante encontrarán el recuadro Para recordar (pág. 6) en el que se sistematizan estas definiciones, se establecen relaciones entre ángulo recto y perpendicularidad, entre ángulo no recto y oblicuidad, y entre rectas que no se cruzan y paralelismo.

Para recordar (pág. 6)

Los problemas 3 a 5 de este apartado buscan abonar estas ideas que luego serán recuperadas para las construcciones de diversas figuras en las que se pone en juego el paralelismo y la perpendicularidad entre segmentos. 

Los problemas incluidos en la sección Para revisar y seguir pensando (pág. 8) apuntan a poner en uso las condiciones de perpendicularidad, oblicuidad y paralelismo para relacionarlas con otras cuestiones que posiblemente los estudiantes ya conozcan. Se propone analizar si existe o no un triángulo o un cuadrado que cumpla las características indicadas, y se espera que las y los estudiantes puedan escribir algunas conclusiones, por ejemplo, “no importa cómo es el triángulo, nunca podrá tener dos lados paralelos porque si no, no se forma el triángulo”, o “hay triángulos con lados perpendiculares, pero solo dos lados”, entre otras.

Los problemas 6 y 7 (pág. 9) presentan instructivos en los que se incluyen las nociones de perpendicularidad, oblicuidad y paralelismo para construir figuras; será necesario usar los instrumentos que permitan trazar los segmentos pedidos. Las instrucciones deberían llevar a que se construyan un paralelogramo y un rectángulo, respectivamente, sin embargo, no se pretende en este momento de la enseñanza que se formalicen ni memoricen sus nombres. Estas construcciones podrían ser retomadas más adelante, cuando se comience el trabajo específico sobre las figuras mencionadas. Por ejemplo, el problema 6 (pág. 9), en el que se requiere interpretar el instructivo para completar el dibujo dado, no se busca que identifiquen la figura formada, sino que pongan en juego las relaciones de paralelismo entre segmentos.

El apartado Estudiar algunas características de los paralelogramos (pág. 9) se ha separado en tres partes, en cada una se consideran diferentes tipos de cuadriláteros. La primera parte aborda el estudio de los cuadrados; la segunda, de los rectángulos y los rombos y la tercera, de los paralelogramos. Al comienzo de cada parte se presenta un recuadro titulado Para tener en cuenta en los que se incluyen definiciones de cada clase de cuadriláteros y algunas imágenes que los representan. Los dibujos incluidos son solo algunos de los representantes posibles dado que hay infinidad de cuadrados, rectángulos, rombos y paralelogramos. Incluso, y es algo que se pretende estudiar a lo largo de este material, existen solapamientos entre las definiciones: podemos considerar al cuadrado como un rombo, un rectángulo o un paralelogramo (dado que para que un cuadrilátero sea considerado rombo debe tener sus cuatro lados de la misma medida, y el cuadrado cumple esta condición; para que sea rectángulo debe tener sus cuatro ángulos rectos y el cuadrado también cumple con esta condición; y del mismo modo el cuadrado es también una clase de paralelogramos).

Las construcciones constituyen una oportunidad potente para indagar propiedades de las figuras, analizar la cantidad de soluciones según los datos que se tienen y buscar argumentos basados en las características conocidas que permitan determinar que la figura cumple con ciertas propiedades. En este caso no se mencionan los instrumentos geométricos habilitados al inicio del apartado sino que se especifican en algunos de los problemas. Así, se limita su uso en algunos casos con intenciones particulares, por ejemplo, poner de relieve ciertas propiedades por sobre otras (los problemas en los que están habilitadas la regla y la escuadra permiten resaltar cierta relación de paralelismo –como entre los lados de los paralelogramos en general– o de perpendicularidad –como entre los lados de los rectángulos–). 

En aquellos problemas en los que está habilitado el compás, se quiere poner en juego la igualdad entre las longitudes de los lados. Por ejemplo, en el problema 1 (pág. 10) se solicita construir un cuadrado usando compás y escuadra de manera que sea la perpendicularidad de los lados lo que rige la construcción, y el compás se incluye para asegurar lados del mismo largo que el segmento ofrecido, sin que sea necesario cuantificar su medida. Así la elección de los instrumentos permitirá poner el foco en propiedades diferentes, por ejemplo, el transportador y la escuadra para trazar los cuatro ángulos rectos. En el problema 2 (pág. 11) se pide construir el cuadrado usando transportador y regla graduada. Esta vez la regla se admite porque el dato es la medida de los lados y no un segmento. El transportador será usado para asegurar ángulos rectos entre lados consecutivos. En estos dos problemas se solicita que las y los estudiantes escriban qué tuvieron en cuenta para asegurar que la construcción efectivamente es un cuadrado y se espera que puedan remitirse a la perpendicularidad y a la igualdad de los lados: “es un cuadrado porque los ángulos son todos rectos como la escuadra, y los lados son iguales porque usamos el compás”. 

En la primera sección de este apartado Para revisar y seguir pensando (pág. 11) se trabaja sobre cuadrados. Con el primer ítem se busca analizar la necesidad de asegurar los ángulos rectos en los cuadrados, por eso no alcanza con usar regla para su construcción. Con el segundo ítem se busca que puedan empezar a relacionar a los cuadrados con los paralelogramos, aun cuando no se espera que se nombren de esa manera. El enunciado dice:

Cabe destacar que este segundo problema tiene relación directa con uno de los problemas presentados en la página 6 de este material. Allí, en la sección Para resolver y seguir pensando (pág. 8) del apartado Rectas y segmentos paralelos y perpendiculares (pág. 4), el primer problema (pág. 8) propone:

La imagen y el inicio de la consigna para ambos problemas es la misma. Se busca que el trabajo presentado en las primeras situaciones con cuadrados constituya un anclaje para abordar este nuevo problema y que la discusión planteada en relación al problema del apartado de Rectas y segmentos paralelos y perpendiculares brinde argumentos sobre las condiciones de paralelismo y perpendicularidad en la construcción de cuadrados.

En la página 12 se presenta el segundo recuadro Para tener en cuenta, esta vez incluyendo definiciones y representaciones de rombos y rectángulos. Notarán que hemos escogido para ambos tipos de cuadriláteros un “representante” en común, el cuadrado, destacando especialmente una característica de él en cada caso. La intención es seguir poniendo en evidencia la relación entre rombos, rectángulos y cuadrados. Algunos de los problemas que siguen en este material permiten analizar dichas relaciones.

Para tener en cuenta (pág. 12)

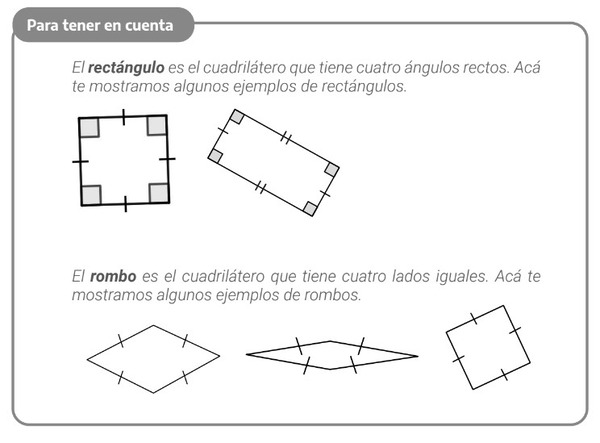
En los primeros problemas sobre rectángulos y rombos se limita el uso de algunos instrumentos geométricos con el propósito de resaltar algunas características en particular, similar a lo mencionado para cuadrados. Así, por ejemplo, en el problema 3 (pág. 12-13) se solicita construir un rectángulo usando escuadra de manera que sea la condición de perpendicularidad de los lados la que motoriza esa tarea; en este sentido, la escuadra permite asegurar los ángulos rectos y el trazado de segmentos. Cabe mencionar que diferentes estudiantes podrán construir rectángulos variados, pues no se informa la medida de los lados consecutivos. Así, las y los estudiantes deberán decidir qué longitud tendrán dichos segmentos, pudiéndose dar el caso particular del cuadrado. Si ningún estudiante incluyera el caso de los lados iguales, esta solución podría ser propuesta por la o el docente para plantear su análisis. 

En el problema 4 (pág. 13) se pide ubicar el cuarto vértice usando sólo el compás, de esta manera se pone de relieve la igualdad de lados opuestos. La construcción es única pues habrá un solo punto de intersección entre los arcos de circunferencia que deberán trazar para ubicar el cuarto vértice. 

Para continuar el estudio de los cuadriláteros se propone trabajar sobre los rombos, comenzando con una copia en el problema 6 (pág. 14). Al resolver esta tarea será necesario tener en cuenta algunas características propias de la figura que inicialmente funcionan de manera implícita pero luego, a partir del pedido del ítem b-, deberán explicitarse. En este punto se espera que se produzca un intercambio general en el que se analicen las diferencias en las estrategias de reproducción, pero también se reflexione sobre lo escrito, para analizar si la información registrada es suficiente y pertinente.  Por ejemplo, es posible que algunas chicas y algunos chicos escriban “fui trazando las líneas con la regla”, lo que no describe en profundidad los pasos seguidos ni explicita las características de la figura puestas en juego. Podrían elegirse algunos registros de la clase y analizarlos grupalmente para agregar información que consideren necesaria o mejorar el modo en que se anotan los pasos.

Los problemas 7 y 8 (pág. 15) parecen similares pues demandan ubicar el cuarto vértice del rombo, sin embargo, se apoyan en cuestiones diferentes. El problema 7 se basa en el paralelismo de los lados opuestos del rombo (por eso se solicita usar regla no graduada y escuadra), en cambio, el problema 8 se basa en la igualdad de dichos lados (por eso se solicita usar el compás). Podría generarse un momento de análisis colectivo en el que se discuta que ambas estrategias se relacionan, que el paralelismo de los lados implica su igualdad, que la igualdad de los lados determina que son paralelos; y aunque no se pretendan demostraciones rigurosas, estas cuestiones pueden escribirse como conclusiones. Más adelante, estas producciones ayudarán a sostener que los rombos son paralelogramos con una característica especial: sus cuatro lados miden lo mismo.

En el problema 9 (pág. 15-16), la intención de limitar la construcción usando solo regla y escuadra se basa en aprovechar el paralelismo de los lados opuestos, ya que con estos dos instrumentos geométricos es posible trazar segmentos paralelos entre sí (cuestión que ya se propuso en problemas anteriores). Nuevamente hemos incluido una pregunta referida a la cantidad de construcciones posibles con los datos dados. Será interesante coordinar un intercambio, luego de las respuestas individuales de las y los estudiantes, para comparar producciones diferentes entre sí. Entre ellas es posible que se encuentre un cuadrado; de ser así será relevante ponerlo a consideración y retomar la conclusión de que el cuadrado es un rombo particular. En caso de que ningún estudiante haya construido un cuadrado, podrá ser la maestra o el maestro quien lo proponga para discutirlo, analizarlo y registrarlo como una conclusión.

En la sección Para revisar y seguir pensando (pág. 16) se incluye una situación que intenta recuperar las posibles discusiones acerca de algunas características de los cuadriláteros estudiados hasta este momento. Además, busca poner el foco en aquellas que son compartidas por distintos cuadriláteros, por ejemplo, en el ítem a- la igualdad de los cuatro lados es una característica que comparten rombos y cuadrados.

En la página 17 se presenta el tercer recuadro Para tener en cuenta, esta vez incluyendo definiciones y representaciones de paralelogramos. Si bien es posible definir los paralelogramos de diversas maneras, se ha optado aquí por establecer que son cuadriláteros que tienen dos pares de lados paralelos e iguales. Los rectángulos, los cuadrados y los rombos son paralelogramos particulares porque cumplen con esa propiedad. Por ejemplo, si los lados paralelos de un paralelogramo forman ángulos rectos, es un rectángulo; si los lados son todos iguales, es un rombo; si los lados son todos iguales y los ángulos interiores son rectos, es un cuadrado. Algunos de los problemas que siguen propondrán analizar dichas relaciones de inclusión.

Para tener en cuenta (pág. 17)

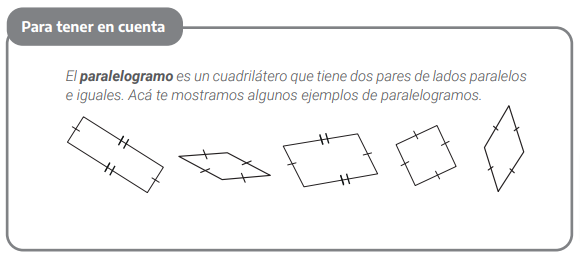
Para continuar el estudio de los cuadriláteros se propone trabajar sobre los paralelogramos. Una vez más, una situación de copiado como la que plantea el problema 10 (pág. 17) permitirá poner en juego algunas características de los distintos cuadriláteros ya trabajados. Nótese que aquí no se limita el uso de instrumentos geométricos particulares con la intención de que esa elección les permita a las niñas y a los niños explicitar algunas características de los paralelogramos, solicitadas en el ítem b-. En este punto se espera que se produzca un intercambio general en el que se analicen las diferencias en las estrategias de reproducción, pero también se reflexione sobre lo escrito, para avanzar en la suficiencia y pertinencia de los registros. 

Los problemas 11 y 12 (pág.17-18) demandan construcciones de paralelogramos, y es importante mencionar que ese término define a un conjunto de cuadriláteros (con los que se trabaja en estos problemas) y también al cuadrilátero específico que no es ni rectángulo, ni rombo, ni cuadrado y tiene dos pares de lados paralelos e iguales. Es por ello que en el problema 11 las dos construcciones solicitadas determinan paralelogramos que no son ni rombos ni rectángulos⁴. En el problema 12 se habilita la posibilidad de construir, entre otras opciones, un rectángulo, pues no se plantea condición alguna sobre los ángulos interiores. Con estas situaciones se promueve la discusión referida a que, al solicitar la construcción de un paralelogramo, según qué datos sean dados, se puede obtener un rombo, un rectángulo, un cuadrado o un paralelogramo que no sea ni rombo ni rectángulo.

Es necesario resaltar la solicitud de realizar las construcciones del problema 11 (pág. 17-18) usando diferentes instrumentos geométricos con la intención de poner de relieve ciertos atributos de los paralelogramos. Así, con el ítem a- se quiere resaltar la condición de paralelismo entre los lados opuestos, con el ítem b- el foco está en la igualdad entre los lados opuestos y con el ítem c- se busca que las y los estudiantes puedan explicitar las dos características mencionadas de los paralelogramos. Es posible que algunas niñas o algunos niños intenten dibujar el paralelogramo “a ojo” usando sólo la regla no graduada, de esta manera los lados “parecerían” paralelos e iguales aun cuando el uso de los instrumentos de construcción no consideró esas características. Será necesario analizar de manera colectiva si se puede garantizar que se trata de un paralelogramo sin haber tenido en cuenta las características de la figura. 

En el problema 12 (pág. 18) es necesario habilitar el uso de la regla graduada por los datos numéricos que se ofrecen. El compás puede ser usado, luego de trazar dos lados consecutivos de 3 cm y 5 cm, para ubicar el cuarto vértice como se hizo, por ejemplo, en el problema 4 de la página 9 de este mismo apartado. Presentamos a continuación posibles construcciones para el problema 12:

12. a- Construí un paralelogramo que tenga dos lados de 3 cm y dos lados de 5 cm, usando regla graduada y compás.

b- ¿Se puede obtener otro paralelogramo diferente con dos lados de 3 cm y dos de 5 cm? Explicá cómo lo pensaste.

Este problema permite volver sobre el anterior. Mientras que en el problema 11 se puede formar solo un paralelogramo para cada ítem, en este caso hay más de una construcción posible dado que la amplitud del ángulo entre dos lados consecutivos no está dada y se puede optar por muchas medidas diferentes.

En los problemas 13 a 16 (pág. 19-21), que completan este apartado, se busca volver sobre las características de los paralelogramos poniendo en juego las condiciones de paralelismo, perpendicularidad e igualdad de lados, remarcando la inclusión entre los diversos tipos de paralelogramos. El problema 13 (pág. 19-20) plantea la construcción de cuadriláteros a partir de interpretar y seguir instrucciones. Serán importantes las intervenciones docentes para acompañar la interpretación de cada instructivo, por ejemplo, el instructivo del ítem a- plantea:

13. a-

Podría surgir una construcción, como la que presentamos en la imagen, en la que se traza un segmento AC, luego el segmento AB oblicuo a éste y por último el segmento BD paralelo e igual a  . En este caso queda determinado un cuadrilátero cóncavo. Será necesario poner en discusión que este tipo de construcción responde al instructivo aunque se trate de una clase de cuadriláteros diferentes de los que se han venido estudiando. 

Una posible construcción correcta, entre muchas, se presenta en la imagen que sigue.

Se podría proceder de igual manera para el resto de los ítems propuestos en el problema 13. El ítem e- propone analizar el tipo de figuras que quedaron formadas en los ítems anteriores y apelar a las características que se han estudiado para fundamentar las respuestas. Se espera entonces que puedan dar razones de por qué en el ítem a- se formó un paralelogramo, en el ítem b- un rectángulo, en el ítem c- un rombo y en el d- un cuadrado. En los problemas 14 y 15 (pág. 21) se espera que las y los estudiantes puedan recuperar algunas de las características que comparten los paralelogramos con los rectángulos y los rombos apuntando a un tratamiento más inclusivo de lo que define a cada clase de cuadriláteros. Por ejemplo, podrían decir que tanto los rectángulos como los rombos tienen lados opuestos paralelos e iguales, lo mismo que los paralelogramos. Y, además, que hay paralelogramos que tienen los cuatro lados del mismo tamaño, como los rombos; así como hay paralelogramos con sus cuatro ángulos rectos, como los rectángulos. La discusión general llevada adelante luego de las resoluciones de estos dos problemas podría propiciar el reconocimiento de que el cuadrado entonces comparte características con el paralelogramo, debido a que se incluye dentro de las definiciones de los rombos y de los rectángulos. Otra posibilidad es dejar esta discusión para después de resolver el problema 16 (pág. 21), ante el cual posiblemente haya quienes afirmen que la construcción no es correcta porque se trata de un rectángulo (se aseguran ángulos rectos por las marcas realizadas).

En la sección Para revisar y seguir pensando (pág. 22) se incluyen prácticas de estudio que recuperan las discusiones acerca de algunas características de los cuadriláteros analizados hasta este momento. Se apunta a que las y los estudiantes exploren y expliciten de un modo sistemático algunas características de los cuadriláteros, así en la situación que se plantea ENTRE TODAS Y TODOS (pág. 22) se espera que puedan volver sobre lo trabajado en los problemas anteriores.

Podría ser momento del armado de algún afiche en forma colectiva resaltando las características trabajadas hasta el momento, como se propone en esta tarea.

Nótese que no se han presentado situaciones en las que se discutan las características de las diagonales ya que serán propuestas más adelante.

En Problemas para estudiar las diagonales de los cuadrados y de los rectángulos (pág. 23) se propone comenzar el estudio de las diagonales de dos tipos de cuadriláteros, estudio que se profundiza en el apartado siguiente a propósito de rombos y paralelogramos. Se inicia con un recuadro Para recordar en el que se representa un cuadrilátero cualquiera que tiene trazada una diagonal. Podría discutirse con las y los estudiantes acerca de que las diagonales son segmentos que quedan por dentro de las figuras y que necesariamente comienzan y terminan en un vértice (podrán remitirse al primer apartado y notar que allí ya trazaron diagonales al realizar las copias). 

Nos interesa remarcar que las situaciones que se proponen en este apartado tienen el propósito de explorar las características de las diagonales de los distintos cuadriláteros, por esa razón, no se presentan inicialmente. Se espera contribuir para que las chicas y los chicos concluyan que las diagonales de los cuadrados son iguales, perpendiculares y se cortan en el punto medio, mientras que las diagonales de los rectángulos son iguales y se cortan en su punto medio. 

El problema 1 (pág. 23-24) busca el establecimiento de relaciones entre lo que las y los estudiantes ya saben de triángulos para avanzar con algunas conjeturas acerca de las diagonales del cuadrado. Nótese que vuelve a entrar en escena un triángulo rectángulo isósceles. Las maestras y los maestros podrían recuperar lo trabajado en el problema 2 (pág. 25) del apartado Estudiar algunos cuadriláteros acerca de la construcción de un cuadrado a partir de un triángulo. Este problema propone la discusión centrada en la diagonal de un cuadrado con el fin de establecer una relación entre el lado  , hipotenusa del triángulo ABC y la diagonal  que quedará determinada luego de construirse el cuadrado. Así se presenta el problema 1 (pág. 23-24).

Se busca que las y los estudiantes expliciten las relaciones que saben sobre los triángulos en este problema de cuadriláteros, entonces podrían responder al ítem b- diciendo para la primera afirmación que es verdadera “porque dos lados miden lo mismo y un ángulo es recto, eso se ve en la imagen del triángulo dado, y el otro triángulo será igual”. Para la segunda afirmación podrían decir que es verdadera “porque la suma de los tres ángulos debe ser 180º, uno es 90º, y 180º menos 90º es 90º”. Para la tercera, necesitarán remitirse a una característica de los triángulos isósceles que no suele recordarse: no solo dos lados miden lo mismo, también dos ángulos. 

El problema 2 (pág. 25) es similar al problema 1 pero debe formarse un rectángulo no rombo. La construcción podría apoyarse en que los lados opuestos del rectángulo son iguales, por lo tanto, el triángulo a dibujar debe ser idéntico al dado pero “girado”. Puede surgir la duda -si no la presentan las y los estudiantes la puede poner en discusión la o el docente- sobre los ángulos del rectángulo, ya que por definición deben ser todos rectos; así, podrá asegurarse que hay dos que lo son, pues el triángulo ofrecido y el nuevo dibujado son rectángulos. Para determinar que los otros dos también son de 90º podrían apoyarse en que el ángulo  y el Ĉ sumados deben dar 90º a partir de considerar la suma de los tres ángulos interiores del triángulo ABC de 180º. Podrán tener en cuenta esa información ya que el nuevo triángulo dibujado tiene las mismas amplitudes que el ABC original y queda apoyado un ángulo Ĉ consecutivo a uno Â, es decir, sumados dan 90º. No se espera que se sistematicen términos como “ángulos consecutivos” o “ángulos complementarios”, sino que se utilicen esas ideas de manera exploratoria.

En este apartado se presentan dos secciones Para revisar y seguir pensando (una después del problema 1 y la otra después del 2) que apuntan a analizar las figuras formadas a partir de un cierto procedimiento de construcción, poniendo de relieve las características de las diagonales. Estas situaciones (otras muy similares volverán a aparecer en el siguiente apartado) tienen como objeto discutir las características de las diagonales de algunos cuadriláteros, en esta ocasión, de los cuadrados y de los rectángulos; así como también que las y los estudiantes interpreten los procedimientos de construcción. En la primera de estas secciones (pág. 24-25) se presenta un procedimiento de construcción de un cuadrado a partir de una de sus diagonales. Se espera que las chicas y los chicos puedan discutirlo en parejas y establezcan algunas conclusiones que les permitan afirmar la veracidad o falsedad de las afirmaciones que luego se presentan. Podrían dar algunas explicaciones tales como “las diagonales del cuadrado son iguales”, “las diagonales del cuadrado son iguales y perpendiculares”, “las diagonales forman ángulos rectos y son iguales” o “las diagonales del cuadrado son iguales, se cruzan en el medio y forman ángulos rectos”. En la segunda de estas secciones (pág. 25-26) se presenta un procedimiento de construcción de un rectángulo a partir de una de sus diagonales, y se busca que las y los estudiantes elaboren algunas conclusiones sobre características de las diagonales de los rectángulos. 

El segundo paso de este instructivo demanda el trazado de un segmento oblicuo, que pase por el punto medio y sea más largo que la diagonal dibujada en el primer paso. Por otra parte, en el procedimiento se hace uso de una circunferencia con el objeto de determinar todos los puntos que se encuentran a una misma distancia de un punto dado. Nada de lo recién dicho anticipa que ese segundo segmento constituirá la segunda de las diagonales. Se espera que durante el análisis y el intercambio colectivo puedan surgir estas relaciones y reconocer la pertinencia del uso de la circunferencia. 

Luego de la resolución de las dos secciones de reflexión que comentamos en los párrafos anteriores podría generarse un espacio de discusión entre todas y todos en el que se pongan de relieve las características que interesa sean registradas y recordadas: las diagonales de los rectángulos son de la misma longitud y se cortan en sus puntos medios; si el rectángulo es un cuadrado, además las diagonales serán perpendiculares.

El trabajo que se propone a continuación se centra en considerar que el cuadrado también es un rombo, y que los tres cuadriláteros mencionados son a la vez paralelogramos.

El problema 3 (pág. 26) demanda utilizar y explicitar las características de las diagonales.

Por ejemplo, para dar respuesta al ítem b- las niñas y los niños podrían plantear “es la primera imagen porque en la última los segmentos no son iguales y en la segunda no se forman ángulos rectos”. Sería interesante ir registrando provisoriamente alguna de estas conclusiones durante el intercambio colectivo. Posiblemente pase inadvertido para algunas y algunos que hay dos juegos de segmentos que pueden ser diagonales de rectángulos, el de la izquierda (cuadrado) y el del medio; será necesario, entonces, recuperar las relaciones ya tratadas.

El problema 4 (pág. 27) nuevamente permite poner en discusión que construir un cuadrado puede ser correcto cuando se pide construir un rectángulo; en este caso, como solo se ofrece una de las diagonales del cuadrilátero, serán las niñas y los niños quienes decidan la longitud y la inclinación respecto del segmento dado de la segunda diagonal. Al tomar esta decisión deberán tener en cuenta las características antes trabajadas, en especial que deben medir lo mismo y cruzarse en sus puntos medios. Al considerar la nueva diagonal perpendicular u oblicua al segmento BE estarán determinando rectángulos cuadrados o no.

En el primer problema de la sección de reflexión (pág. 27-28) se solicita analizar la cantidad de construcciones posibles. Será interesante conversar con el grupo clase que, para resolver el ítem b-, hay muchos rectángulos posibles con esa diagonal y uno de ellos es el cuadrado dibujado para el ítem a-. Los tres siguientes problemas tienen la intención de reflexionar sobre las características que deben cumplir las diagonales para que se trate de un cuadrado o de un rectángulo en general. Por ejemplo:

• DE A DOS: Si un cuadrilátero tiene sus diagonales iguales, que se cortan en sus puntos medios de modo no perpendicular, ¿es posible estar seguro de qué cuadrilátero se trata? Discutan cómo lo pensaron.

Ante este problema se espera que puedan decir que la condición “de un modo no perpendicular” elimina de las soluciones a los cuadrados.

Es necesario mencionar que, a lo largo de este apartado, Problemas para estudiar las diagonales de los cuadrados y de los rectángulos, no se presentan las secciones “Para recordar” o “Para tener en cuenta”. En lugar de ofrecer información sobre características de las diagonales de estos tipos de figuras, se busca que las y los estudiantes puedan elaborar sus propias conjeturas. Será interesante proponer su escritura provisoria en afiches para luego, retomarlas, revisarlas y ampliarlas a partir de la exploración de las diagonales de rombos y paralelogramos.

En el siguiente apartado, Problemas para estudiar las diagonales de los rombos y de los paralelogramos (pág. 28), se presenta una serie de situaciones que buscan analizar y construir las características de las diagonales de los rombos y de los paralelogramos. Se proponen problemas en los que hay que construir estas figuras a partir de triángulos, de manera que se utilice uno de sus lados como diagonal del cuadrilátero a dibujar. En otros problemas vuelven a proponerse procedimientos de construcción para debatir y analizar el comportamiento de las diagonales en cada uno de los casos. Además, se trata de analizar los datos que posibilitan la determinación acerca de la cantidad de soluciones. Se espera que las y los estudiantes, luego del trabajo sobre estos problemas y a partir de la coordinación de momentos de intercambio colectivo por parte de la o el docente, puedan dar explicaciones sobre las características de las diagonales de los rombos y de los paralelogramos, registrar en carteles y utilizar dichos registros en nuevos problemas. Así, por ejemplo, podrían plantear: “las diagonales del rombo se cruzan formando ángulos rectos” o “las diagonales del rombo y del paralelogramo se cortan a la mitad”. Al final del apartado se presenta la sección Para tener en cuenta (pág. 33) donde se sintetizan las características de las diagonales de los cuadriláteros estudiados hasta ese momento. Esto puede ser una oportunidad de volver colectivamente sobre la escritura de esas primeras hipótesis para ponerlas en diálogo con estas nuevas ideas.

En los problemas que presenta el apartado Cuadriláteros a partir de lados y diagonales (pág. 34) se busca, a partir de la construcción de distintos cuadriláteros, explicitar relaciones entre lados y diagonales no estudiados hasta el momento. Una vez más se orientan los tipos de instrumentos geométricos que se van a necesitar: regla graduada, compás y escuadra, para poner de relieve algunas características de las figuras sobre otras. Así, por ejemplo, en el problema 1 (pág. 34) se trata de construir un rectángulo y un cuadrado teniendo como dato la diagonal:

Será necesario recurrir a lo estudiado en el apartado anterior para abordar la construcción de ambas figuras tomando como dato la medida de una de las diagonales. Así, un posible procedimiento de construcción del rectángulo sería:

• dibujar un segmento de 6 cm (será una diagonal) en cualquier posición;
• trazar otro segmento de 6 cm (será la otra diagonal) que pase por el punto medio del primero pero que a la vez sea cortado por éste en su punto medio;
• como los extremos de las dos diagonales trazadas conforman los vértices del rectángulo, restaría unirlos con segmentos que serán los lados.

Algo semejante puede suceder con la construcción del cuadrado aunque, en este caso, los segmentos además de ser iguales y cortarse en sus puntos medios deberán formar ángulos rectos. La maestra o el maestro podrá poner a consideración del grupo si las figuras obtenidas son únicas, informando que si la forma es la misma no importa su ubicación en la hoja, se trata de la misma figura. Nótese que no es necesario recurrir a las condiciones de paralelismo o perpendicularidad de lados para asegurarse que la construcción obtenida es un rectángulo o un cuadrado. 

El problema 2 (pág. 34) propone construcciones de paralelogramos para lo que podría ser útil retomar o volver a mirar los afiches con conclusiones creados a partir de apartados anteriores. En cada ítem se ofrecen datos distintos, por lo que será necesario tener en cuenta características diferentes para la construcción. Nuevamente sucede que, como los datos son longitudes de lados y diagonales, se permite la construcción de rectángulos o rombos como representantes posibles de los paralelogramos. Para construir en el ítem a- podrían resaltar el paralelismo o la igualdad entre lados opuestos; la variedad de figuras posible estará determinada por la amplitud del ángulo entre lados consecutivos. En el ítem b- sucede algo similar, las distintas amplitudes posibles para el ángulo entre el lado de 3 cm y la diagonal de 6 cm serán quienes determinen las diversas figuras a construir, entre ellas se encuentra nuevamente un rectángulo. Con el ítem c- será posible construir una gran variedad de paralelogramos, entre los que se encontrará un rombo. Finalmente, con el último ítem se pretende seguir abordando la inclusión entre clasificaciones de cuadriláteros, pues con dos lados de la misma medida se podrán construir rombos o cuadrados. Es posible que algunas y algunos estudiantes no reconozcan inmediatamente esta opción.

Presentamos a continuación algunas construcciones posibles del ítem a-:

Una construcción posible del ítem b- podría partir del trazado del lado de 3 cm, luego la diagonal de 6 cm con cualquier amplitud del ángulo entre ellos, para continuar completando un triángulo al unir los puntos E y G (ver figura que sigue). Una vez hecho esto el problema será similar al propuesto en el apartado Problemas para estudiar las diagonales de los rombos y de los paralelogramos (pág. 28), particularmente el problema 4 (pág. 30), en el que se solicitó la construcción de un paralelogramo a partir de un triángulo dado, sabiendo que uno de sus lados sería la diagonal del paralelogramo a construir. Es decir, podrán remitirse al trazado de paralelas a los lados opuestos.

En la sección Para revisar y seguir pensando (pág. 34) se propone retomar los problemas 1, 2 y 3 para comparar si las producciones de la pareja son iguales. En los problemas 1.b- y 3 las construcciones son únicas, por lo que las realizaciones de la pareja deberían verse igual. Será preciso recordar que, aunque se encuentren en distintas posiciones, se trata de la misma figura si la forma es la misma. En los restantes problemas, los datos admiten diversidad de figuras, será interesante discutir si son o no correctas todas y cuántas soluciones admite cada caso.

En el último problema de esta sección de reflexión solicitamos que agreguen información de la segunda diagonal de manera que pueda asegurarse que se trata del tipo de cuadrilátero mencionado en cada inciso. 

Así, para el primero de los incisos será necesario tener en cuenta que los rectángulos no cuadrados tienen diagonales de la misma longitud, que se cruzan en sus puntos medios y el ángulo que forman al cruzarse no es recto. Para el segundo inciso deberán recordar que los rombos tienen sus diagonales perpendiculares que se cruzan en sus puntos medios, pero al demandar que no sea cuadrado se exige que las diagonales tengan diferentes longitudes. Finalmente, para el tercero de los incisos, habrá que unificar las características antes mencionadas para rectángulos y rombos, es decir, las diagonales deberán ser de la misma longitud, perpendiculares y cruzarse en sus puntos medios.

Es posible que sea necesario conversar con las y los estudiantes acerca de las denominaciones “rectángulo no cuadrado” y “rombo no cuadrado”. Para ponerlo en discusión podrían remitirse a muchos de los problemas ya resueltos a partir de este material y, especialmente, a los registros de conclusiones.

En el siguiente apartado, Problemas para explorar los ángulos de los cuadriláteros (pág. 36), se busca que las y los estudiantes puedan explorar y establecer algunas conjeturas vinculadas a la existencia o no de un cuadrilátero conociendo la medida de sus ángulos. Las situaciones que aquí se incluyen apuntan a construir con ellas y ellos la propiedad que afirma que la suma de los ángulos interiores de todo cuadrilátero equivale a 360º. Así como también poner en juego otras características de los cuadriláteros y triángulos, como por ejemplo: “si se trata de un rectángulo sus ángulos interiores miden 90º”; “si es un triángulo isósceles dos ángulos medirán lo mismo”; “si es un rombo los lados serán de la misma longitud” (lo que llevaría a que se forman triángulos isósceles); “la suma de los ángulos interiores de los triángulos es de 180º”; entre otras posibles. Se trata de introducir a las y los estudiantes en un trabajo deductivo a partir de lo que han construido sobre las características y propiedades de las figuras, sus diagonales y sus ángulos. Para favorecer ese tipo de trabajo en todos ellos se inhibe el uso de instrumentos de medición.

En el problema 1 (pág. 36) se propone trabajar de modo exploratorio. Una forma de iniciar el proceso de resolución podría ser anticipando/eligiendo las medidas de los ángulos que cumplan las condiciones dadas en los incisos a- y c-. Luego, podrían intentar las construcciones y, al no conseguirlo, concluir que “sus lados nunca se van a juntar”, que “el cuadrilátero no cierra” o que “no queda un cuadrilátero”. En el inciso c- hemos escogido que la suma supere los 400º para que haya una diferencia importante respecto de lo necesario para que se pueda construir el cuadrilátero, así no será la imprecisión en los trazados lo que invalide las conclusiones. En cambio, en el inciso a- podrían escoger ángulos agudos pero todos muy cercanos a 90º y, dados los errores de medición con los instrumentos geométricos, conseguir que parezca un cuadrilátero. En esa instancia será interesante volver a conversar acerca de la necesidad de apoyarse en las características de las figuras en lugar de confiar sin reparos en las mediciones. En el ítem b- probablemente logren anticipar que se pueden construir rectángulos o cuadrados; y si no la lograran, la maestra o el maestro podría solicitar que analicen y comparen con los problemas anteriores antes de intentar la construcción. 

El problema 2 (pág. 37) permite explorar que si tres de los ángulos de un cuadrilátero son rectos, el cuarto ángulo no puede ser de cualquier medida. Es posible que las y los estudiantes conjeturen que el cuarto ángulo es de 90º. La maestra o el maestro podría volver sobre esta afirmación y analizar que, si se conoce la medida de tres de los ángulos, la amplitud del siguiente está determinada. 

La situación que se presenta en la sección Para revisar y seguir pensando (pág. 37) apunta a que se establezca que en un cuadrilátero la suma de sus ángulos interiores es 360º apelando a la propiedad de la suma de los ángulos interiores de los triángulos⁴. El problema propone el análisis de este razonamiento para validar la respuesta, sin apoyarse en la medida de los ángulos.

Con los problemas 3 (pág. 38) y 4 (pág. 38) se busca que reutilicen el razonamiento que se empleó en la situación de la sección de reflexión anterior para determinar la medida de los ángulos desconocidos. Para el problema 3 podrían plantear “como la suma de todos los ángulos tiene que ser 360º y aquí los tres ángulos dados suman 282º, entonces el cuarto ángulo será de 78º”; y para el problema 4, “si la suma de los ángulos interiores tiene que ser 360º y con los dos datos se suma 224º, entonces se lo restamos a 360º y nos queda 136º, a esto hay que dividirlo en dos partes iguales porque dice que Ĉ y D̂ miden lo mismo, nos queda 68º”. Una vez más se busca que puedan decidir apelando a argumentos y sin medir.

Se espera que a partir de las discusiones en torno a estas resoluciones las y los estudiantes puedan concluir que los ángulos opuestos en todos los paralelogramos tienen la misma amplitud, y que en algunos casos los ángulos interiores consecutivos pueden medir diferente. Una forma de analizar esta verdad es considerar que en ellos, al trazar una de las diagonales, quedan determinados dos triángulos iguales.

Presentamos a continuación una posible resolución del problema 5 (pág. 34):

Las y los estudiantes podrían relacionar el triángulo que brinda el dato del ángulo de 40º y argumentar que es isósceles ya que las diagonales de los rectángulos se cortan en sus puntos medios y tienen la misma longitud, entonces los otros dos ángulos también son iguales. Como los ángulos interiores de los triángulos suman 180º, la suma de esos ángulos debe ser 140º (surge de 180º - 40º) por lo que cada uno mide 70º. Ese dato ayuda a buscar la amplitud de M̂ dado que los ángulos de los rectángulos son rectos -miden 90º-, entonces M̂ debe medir lo que falta desde 70º para llegar a 90º, es decir 20º. 

Presentamos a continuación una posible resolución del problema 6 (pág. 39):

Para este rombo, los ángulos N̂ y Q̂ son opuestos, por lo que podrán concluir que miden lo mismo a partir de utilizar relaciones estudiadas en problemas anteriores, por ejemplo, decir que los triángulos MNP y MPQ son iguales (dado que los lados del rombo son iguales y comparten el tercer lado -la diagonal-) e isósceles, entonces, en cada triángulo M̂ medirá igual que P̂, es decir 55º. Con esto, y usando que la suma dentro del triángulo debe ser 180º, N̂ mide 70º. Si partieron de considerar la igualdad de triángulos entonces pueden concluir que el ángulo Q̂ también mide 70º. Si no partieran de esa consideración, podrían realizar un estudio similar para el triángulo MPQ y llegar a la conclusión que Q̂ mide 70º. Si este fuese el caso, sería interesante poner en relevancia que los dos ángulos desconocidos miden lo mismo y son opuestos. Luego se podría proponer analizar si sucede lo mismo con los otros ángulos opuestos del rombo, P̂ y M̂. Para complementar estas ideas, la maestra o el maestro podría retomar otras figuras de este material para analizar e intervenir preguntando, por ejemplo, qué sucede con los ángulos opuestos de los rectángulos o de los cuadrados.

Con el siguiente recuadro Para recordar y tener en cuenta (pág. 39) se pretende sistematizar la idea anterior, solo que aquí se presenta extendiendo a todos los paralelogramos, es decir se deja de poner el foco en los rombos, en los rectángulos o en los cuadrados, para dar argumentos más amplios. En los siguientes problemas se pondrán en juego estas ideas.

En el problema 7 (pág. 40) se busca trabajar en torno a las relaciones de igualdad de ángulos opuestos en los paralelogramos y que la suma de los ángulos interiores es 360º. 

Una manera posible de resolver este problema es partir de considerar la igualdad de los ángulos opuestos. Así, para la figura completa, Ŝ y F̂ son opuestos, por lo tanto, iguales; de forma análoga,  y D̂ son opuestos e iguales. Es posible pensar que Ŝ mide 130º -suma de 50º y 80º-, entonces F mide 130º. Como la suma de los ángulos interiores de los cuadriláteros es 360º, y Ŝ más F̂ es 260º, entonces  más D̂ debe ser 100º. Como son iguales por ser opuestos, entonces cada uno medirá 50º. Anticipamos que estas deducciones y conclusiones pueden no surgir rápidamente entre las chicas y los chicos, por lo que podría ser útil un primer acercamiento al problema de manera individual para luego pasar a un trabajo en parejas o ternas, de modo que puedan presentarse debates internos, exposición de estrategias o de ideas, búsqueda de conclusiones al menos parciales.

Como hemos mencionado anteriormente puede ser útil para las y los estudiantes sistematizar lo trabajado escribiendo cuadros con algunas conclusiones, propiedades y características de las figuras. A modo de ejemplo, les ofrecemos a continuación un cuadro que podría elaborarse en las aulas.

Los problemas que presenta la sección Para revisar y seguir pensando (pág. 40-41) buscan recapitular el trabajo sobre el estudio de cuadriláteros, a la vez que sistematizar las ideas que fueron surgiendo. Particularmente esto puede verse en el último de los ítems, propuesto para resolver entre todas y todos en la clase. Se trata de una tabla en la que se han escrito características de los cuadriláteros y se solicita determinar cuál o cuáles de los diferentes tipos de éstos las cumplen. Será necesario recordar a las y los estudiantes que hay relaciones de inclusión entre las figuras del cuadro y que, por lo tanto, deberán considerarse las figuras más generales y no solo algunos ejemplos en particular.

Los intercambios grupales que pudieran surgir en torno al cuadro, podrían redactarse como ideas que les permitieran a las y los estudiantes volver sobre ellas en otras oportunidades, como por ejemplo en momentos de evaluación. Ofrecemos a continuación una posible síntesis de las mismas.

Con los problemas de las páginas anteriores estuvimos trabajando sobre las siguientes ideas:

En este documento hemos intentado acompañar el análisis de los problemas del material para estudiantes. Esperamos que su lectura constituya un aporte para la planificación y la coordinación de las clases.

---

¹ En este documento y en el material para estudiantes, hemos optado por referirnos a los segmentos utilizando la notación “extremos del segmento” con una rayita sobre las letras.

² Si bien en hojas cuadriculadas se puede volver necesaria la consideración de la perpendicularidad de lados consecutivos de un rectángulo si no se construye siguiendo el cuadriculado de la hoja, reservamos su uso para cuando sí coinciden los lados de las figuras con el cuadriculado.

³ En algunas publicaciones para estudiantes y para docentes, a estas figuras se las denomina “paralelogramo propiamente dicho”. En este material no usaremos dicha denominación con las y los estudiantes con el fin de que no se desdibujen las relaciones de inclusión, es decir que rombos, rectángulos y cuadrados son también paralelogramos.  

⁴ Esta propiedad fue tratada en la Parte 3 de este material sobre el estudio de la geometría.